Помогите пожалуйста, с рисунками желательно
7 класс
К-3, В-1
1. Отрезки EF и PQ пересекаются в их середине М. Докажите, что
РЕ | QF.
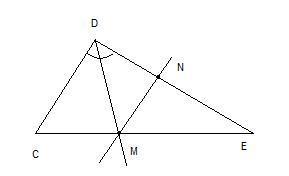
2. Отрезок DM биссектриса треугольника CDE. Через точку м
проведена прямая, параллельная стороне CD и пересекающая сторону DE в точке N. Найдите углы треугольника DMN, если <СDE = 68°.
Ответы на вопрос
Ответил julypolly2006
2
Ответ:
на фото ответ
Объяснение:
второе задание:
1. После построения MN получается треугольник MNE, подобный треугольнику CDE по первому признаку подобия (угол Е - общий, углы С и NME равны как соответственные углы при пересечении двух параллельных прямых CD и MN секущей СЕ). Поскольку треугольники подобны, то
<MNE = <CDE = 68°
2. Зная, что развернутый угол равен 180°, находим угол DNM:
<DNM = 180 - <MNE = 180 - 68 = 112°
3. Поскольку DM - биссектриса, то угол MDN = <CDE : 2 = 68 : 2 = 34°
4. Зная два угла треугольника DMN, находим неизвестный угол:
<DMN = 180 - <MDN - <DNM = 180 - 34 - 112 = 34°
Приложения:

Nastaa124:
можешь, пожалуйста, ко 2 заданию написать дано, и что требуется доказать?
Новые вопросы
Английский язык,
1 год назад
Немецкий язык,
2 года назад
Математика,
2 года назад
Математика,
7 лет назад