Помогите пожалуйста с решением задачи!

Ответы на вопрос
Боковая сторона равнобедренного треугольника равна 10 см, а высота к основанию - 8 см. Через вершину угла при основании проведена прямая. делящая высоту в отношении 3:1, считая от вершины. Найдите длину отрезка этой прямой, заключённого внутри данного треугольника.
——————————————
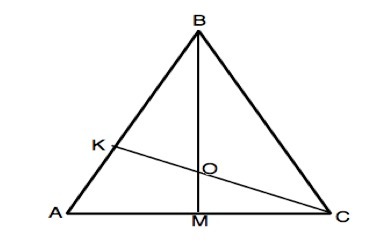
Обозначим треугольник АВС, его высоту - ВМ.
Отрезок прямой СК, точку его пересечения с высотой - О.
Высота равнобедренного треугольника является его медианой и делит ∆ АВС на два равных прямоугольных.
В ∆ АВМ катет АМ=6 см ( тр-к египетский, проверьте по т.Пифагора).
ВО=3 части, ОМ=1ч.
ВМ=4 части. ОМ=8:4=2, ВО=8:4•3=6
По т. Менелая
Откуда
АВ=2ч+3ч=5 частей
АК=10•2/5=4
По т.косинусов
КС²=АК²+АС²-2АК•АС•cos∠KAC
cos∠KAC=cosBAC=AM:AB=0,6
СK²=4²+12²-2•4•12•0,6
CK=√102,4 ≈10,1193 см