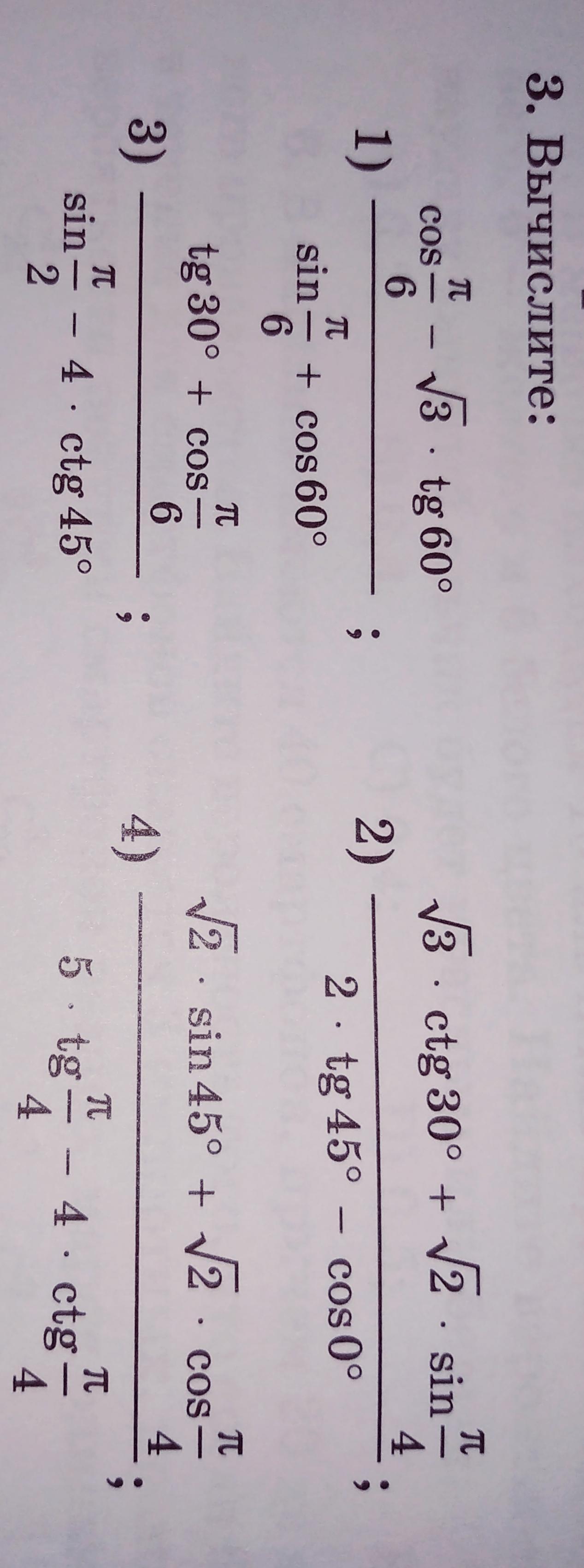
Алгебра, вопрос задал AyeHeyviSoon , 2 года назад

Помогите, пожалуйста, с решением, даю 100 баллов. Буду очень благодарен, могу поставить высшие оценки. Только, пожалуйста, не стоит ничего писать, если не имеете понятия в решении задачи.

Приложения:

Ответы на вопрос

Ответил Miroslava227

Ответ:

$\frac{ \cos( \frac{\pi}{6} ) - \sqrt{3} tg(60^{\circ} )}{ \sin( \frac{\pi}{6} ) + \cos(60^{\circ} ) } = \frac{ \frac{ \sqrt{3} }{2} - \sqrt{3} \times \sqrt{3} }{ \frac{1}{2} + \frac{1}{2} } = \\ = (\frac{ \sqrt{3} }{2} - 3) \div 1 = \frac{ \sqrt{3} }{2} - 3$

$\frac{ \sqrt{3}ctg(30^{\circ} ) + \sqrt{2} \sin( \frac{\pi}{4} ) }{2tg(45^{\circ} ) - \cos(0^{\circ} ) } = \frac{ \sqrt{3} \times \sqrt{3} + \sqrt{2} \times \frac{ \sqrt{2} }{2} }{2 \times 1 - 1 } = \\ = \frac{3 + 1}{1} = 4$

$\frac{tg(30^{\circ} ) + \cos( \frac{\pi}{6} ) }{ \sin( \frac{\pi}{2} ) - 4ctg(45^{\circ} ) } = \frac{ \frac{ \sqrt{3} }{3} + \frac{ \sqrt{3} }{2} }{1 - 4 \times 1} = \\ = (\frac{2 \sqrt{3} }{6} + \frac{3 \sqrt{3} }{6} ) \times ( - \frac{1}{3} ) = - \frac{5 \sqrt{3} }{18}$

$\frac{ \sqrt{2} \sin(45^{\circ} ) + \sqrt{2} \cos( \frac{\pi}{4} ) }{5tg \frac{\pi}{4} - 4ctg \frac{\pi}{4} } = \frac{ \sqrt{2} \times \frac{ \sqrt{2} }{2} + \sqrt{2} \times \frac{ \sqrt{2} }{2} }{5 - 4} = \\ = 1 + 1 = 2$

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Українська література, 1 год назад

твір роздум про герасима калитку...

Українська мова, 1 год назад

агроном, комбайн, комбайнер, фермер, скласти речення з цими словами які вказують на завершену дію.

Математика, 2 года назад

У нас есть 25 штук по 10 и 50 тенге. Если сумма всего 530 тенге, сколько 10 тенге в этой монете?

Русский язык, 2 года назад

помогите(и да снова)...

Математика, 8 лет назад

из 112 кг. руды получают 84 кг. железа. сколько килограммов железа получит из 64 кг.руды?

Математика, 8 лет назад

В магазине было 550 бытовых приборов:60 телевизоров,50 видеоплееров,а остальные компьютеры.Сколько компьютеров было в магазине?поогите решить,еще с уравненем.