Алгебра, вопрос задал Аноним , 1 год назад

Помогите пожалуйста с решением ​

Приложения:

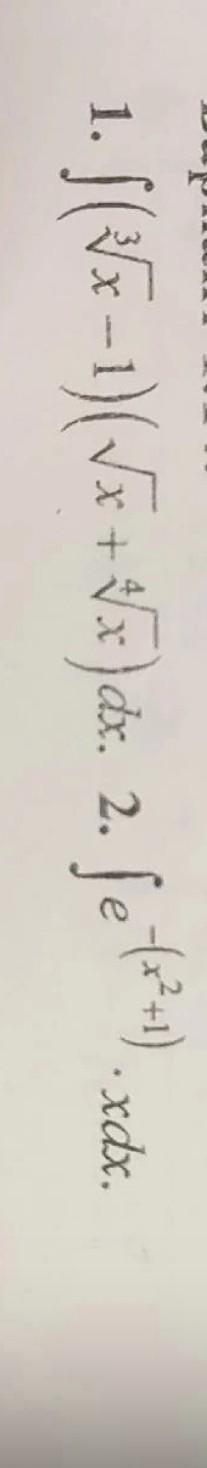
Ответы на вопрос

Ответил Alnadya
0

Решение.

1) Сначала упрощаем подынтегральное выражение.

\bf \displaystyle \int (\sqrt[3]{x}-1)(\sqrt{x}+\sqrt[4]{x})\, dx=\int (x^{^{\frac{5}{6}}}+x^{^{\frac{7}{12}}}-x^{^{\frac{1}{2}}}-x^{^{\frac{1}{4}}})\, dx=\\\\\\=\frac{x^{^{\frac{11}{6}}}}{11/6}+\frac{x^{^{\frac{19}{12}}}}{19/12}-\frac{x^{^{\frac{3}{2}}}}{3/2}-\frac{x^{^{\frac{5}{4}}}}{5/4}+C=\frac{6\, x^{^{\frac{11}{6}}}}{11}+\frac{12\, x^{^{\frac{19}{12}}}}{19}-\frac{2\, x^{^{\frac{3}{2}}}}{3}-\frac{4\, x^{^{\frac{5}{4}}}}{5}+C

2)  Подведение под знак дифференциала .

\bf \displaystyle \int e^{-(x^2+1)}\, x\, dx=\int e^{-x^2-1}\cdot \frac{d(-x^2-1)}{-2}=-\frac{1}{2}\cdot e^{-x^2-1}+C=e^{-(x^2+1)}+C\\\\\\{}\ \ \star \ \ d\, (-x^2-1)=(-x^2-1)'\, dx=-2x\, dx\ \ \star

Предыдущий вопрос
Следующий вопрос
Новые вопросы
Химия, 1 год назад
У ряду атомів хімічних елементів Li - Be - B - C * збільшується електронегативність збільшується загальне число електронів збільшуються металічні властивості збільшується радіус збільшується...
Биология, 1 год назад
До мікроелементів належить: 1.Ферум 2.Йод 3.Оксиген 4.Кальцій 2 ОТВЕТА!!!
Английский язык, 1 год назад
Помогите пожалуйста срочно даю 20 балов...
Химия, 1 год назад
Какой из этих металлов имеет наивысшую среди металлов тепло- и электропроводность? а) медь б) серебро в) золото г) цинк​...
География, 6 лет назад
Альпинист решил подняться на гору Эльбрус, абсолютная высота которой 5642м. Какая температура воздуха на вершине горы, если температура воздуха у ее подножия (абсолютная высота 2000м) +12С?
Математика, 6 лет назад
На новогоднем празднике каждый ученик 8 класса подарил маленькие подарки всем своим одноклассникам. Сколько человек учится в этом классе, если всего на празднике было вручено 342 подарка?​