Помогите пожалуйста с геометрией чертёж и подробное решение

Ответ:ВН

Sбок = 3S(√3+1)/2.

Объяснение:

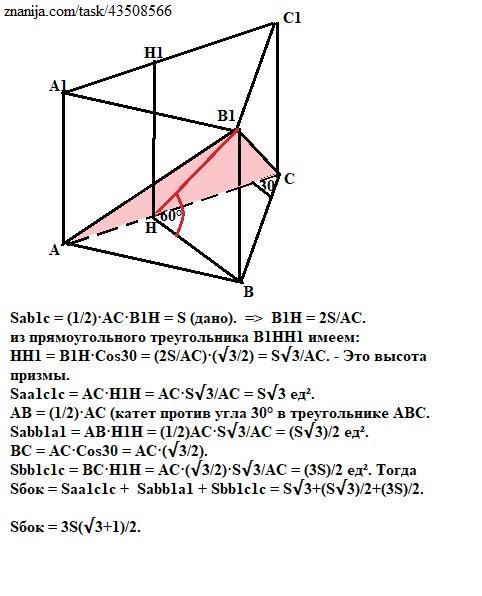
Sab1с = (1/2)·AC·B1H = S (дано).  =>  В1Н = 2S/AC.

Угол между двумя пересекающимися плоскостями (двугранный угол)  равен углу между прямыми, по которым они пересекаются с любой плоскостью, перпендикулярной их линии пересечения.

Проведя высоты В1Н и ВН в треугольниках АВС и А1В1С1 соответственно  (основания этих перпендикуляров совпадут по теореме о трех перпендикулярах) , получим прямоугольный треугольник В1НВ с углом ∠ВНВ1 = 60° (дано).

Из прямоугольного треугольника В1НН1 с углом Н1НВ1 = 30° (так как ∠Н1НВ=90°) имеем:

HH1 = B1H·Cos30 = (2S/AC)·(√3/2) = S√3/AC. - Это высота призмы.  

Saa1c1c = AC·H1H = AC·S√3/AC = S√3 ед².

AB = (1/2)·AC (катет против угла 30° в треугольнике АВС.

Sabb1a1 = AB·H1H = (1/2)AC·S√3/AC = (S√3)/2 ед².

ВС = АС·Cos30 = АС·(√3/2)  (из треугольника АВС).

Sbb1с1с = ВС·H1H = АС·(√3/2)·S√3/AC = (3S)/2 ед². Тогда

Sбок = Saa1c1c +  Sabb1a1 + Sbb1с1с = S√3+(S√3)/2+(3S)/2.

Sбок = 3S(√3+1)/2.