Помогите пожалуйста! С формулами и более развёрнуто, заранее спасибо
Ответы на вопрос
Объяснение:
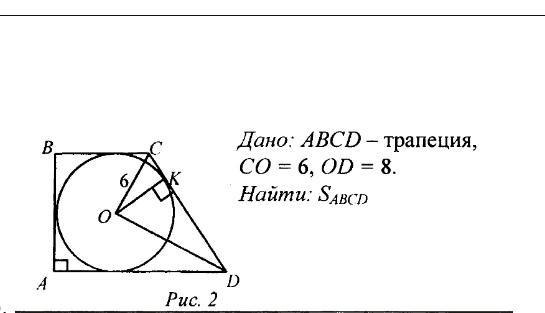
Дано АВСD-описанная прямоугольная трапеция,с основаниями АD и ВС, ∠А=90°, О-центр вписанной окружности , ОС=6, ОD=8 ,ОК⊥СD.
Найти S(трапеции).
Решение.
S(трапеции)=1/2*Р( трапеции)*r, где r-радиус вписанной окружности.
∠COD=90º,
т.к. ∠ADC+∠BCD=180º , как сумма внутренних односторонних углов при AD║ BC и секущей CD. Центр вписанной окружности является точкой пересечения биссектрис углов трапеции ⇒ 1/2*(∠ADC+∠BCD)=90º ⇒∠ОDC+∠ОCD=90º.
ΔOCD ,∠OCD=180°-90°=90°⇒ΔOCD-прямоугольный. По т. Пифагора CD=√(6²+8²)=√100=10.
Т.к. квадрат катета ,в прямоугольном треугольника, равен произведению проекции катета на гипотенузу, то 6²=СК*10 или СК=3,6. Тогда КD=10-3,6=6,4.
Высота,в прямоугольном треугольника, есть среднее
пропорциональное между длинами отрезков, на которые
основание высоты делит гипотенузу⇒ОК=√(3,6*6,4)=4,8.
Т.к. r=4,8 , то d=AB=4,8*2=9,6.
АВ+СD=9,6+10=19,6.
Значит ВС+АD=19,6 т.к суммы длин противолежащих сторон, в описанном 4-х угольнике, равны.
Р(трапеции )=АВ+CD+ВС+AD = 19,6+19,6=39,2 .
S(трапеции)=1/2*39,2*4,8=94,08 (ед²).