Алгебра, вопрос задал Аноним , 2 года назад

помогите пожалуйста решить задачу по алгебре ​

Приложения:

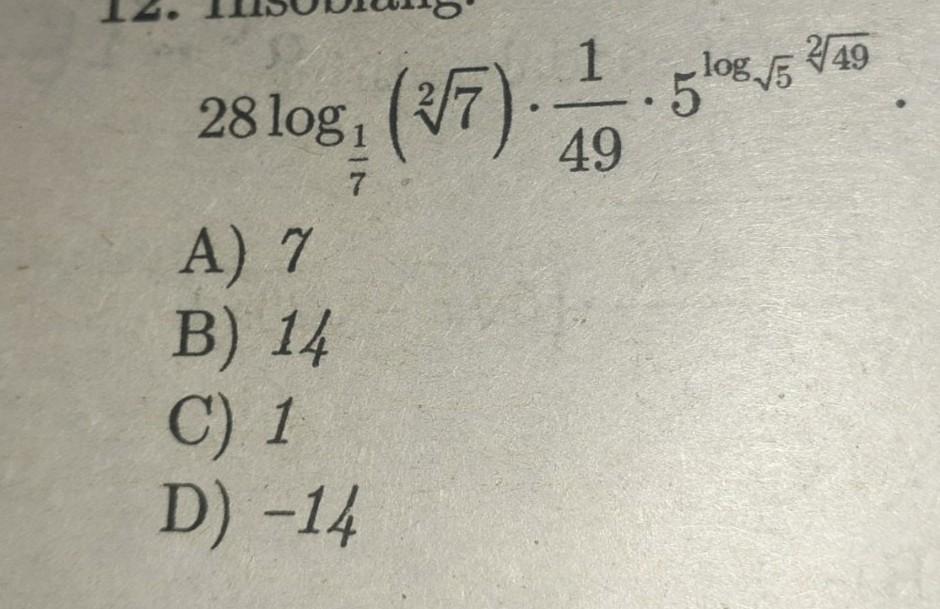
Ответы на вопрос

Ответил tarasabc
0

Відповідь:

-14

Пояснення:

28*log_{\frac{1}{7} }(\sqrt[2]{7} )*\frac{1}{49} *5^{log_{\sqrt{5} }\sqrt[2]{49} }

В даному прикладі використаємо наступні властивості логарифмів:

log_{n^m}a=\frac{1}{m}log_na               log_na^m=mlog_na          a^{log_ab}=b

І такі властивості степенів:        \frac{1}{a^n}=a^{-n}               \sqrt[n]{a} =a^{\frac{1}{n}}

1) Спростимо для початку log_{\frac{1}{7} }(\sqrt[2]{7} )

log_{\frac{1}{7} }(\sqrt[2]{7} )=log_{7^{-1}}7^{\frac{1}{2} }=-1*\frac{1}{2}log_77=-\frac{1}{2}

2) А тепер спростимо 5^{log_{\sqrt{5} }\sqrt[2]{49} }

5^{log_{\sqrt{5} }\sqrt[2]{49} }=5^{log_{5^{\frac{1}{2} } }7}=5^{2log_{5 }7} }=5^{log_{5 }7^2} }=5^{log_{5 }49} }=49

3) А тепер наші спрощені частини підставимо у вираз, і обчислимо його:

28*log_{\frac{1}{7} }(\sqrt[2]{7} )*\frac{1}{49} *5^{log_{\sqrt{5} }\sqrt[2]{49} }=28*(-\frac{1}{2} )*\frac{1}{49} *49=-\frac{28}{2} *\frac{49}{49} =-14

Предыдущий вопрос
Следующий вопрос
Новые вопросы
Английский язык, 1 год назад
Диалог пожалуйста Скажите,что бы вам хотелось улучшить в вашем городе.Используйте:build new modern houses,paint houses in different colours, plant trees and colourful flowers, paint funny pictures...
Українська література, 1 год назад
За змістом останнього речення прочитанного твору складіть нову казку Найприкріше було зимі, що навіть малеча і та її не боїться! Ковзається собі на ковзанах та на санках, у сніжки грається, баб...
Алгебра, 2 года назад
помогите решить уравнение,на уровне 7класса (без корней),дам 10 баллов...
Алгебра, 2 года назад
помогите срочно пожалуйста,дам 15 баллов...
География, 7 лет назад
Тибетский буддистский монастырь Ронгбук (основан в 1902 году) —самое высокое место на Земле, где постоянно живут люди. Легендарный монастырь расположен на северной стороне Гималаев, у подножия...
Обществознание, 7 лет назад
приведите примеры: когда твои потребности удовлетворяются, а потребности других не удовлетворяются...