Помогите пожалуйста решить задачи
Приложения:
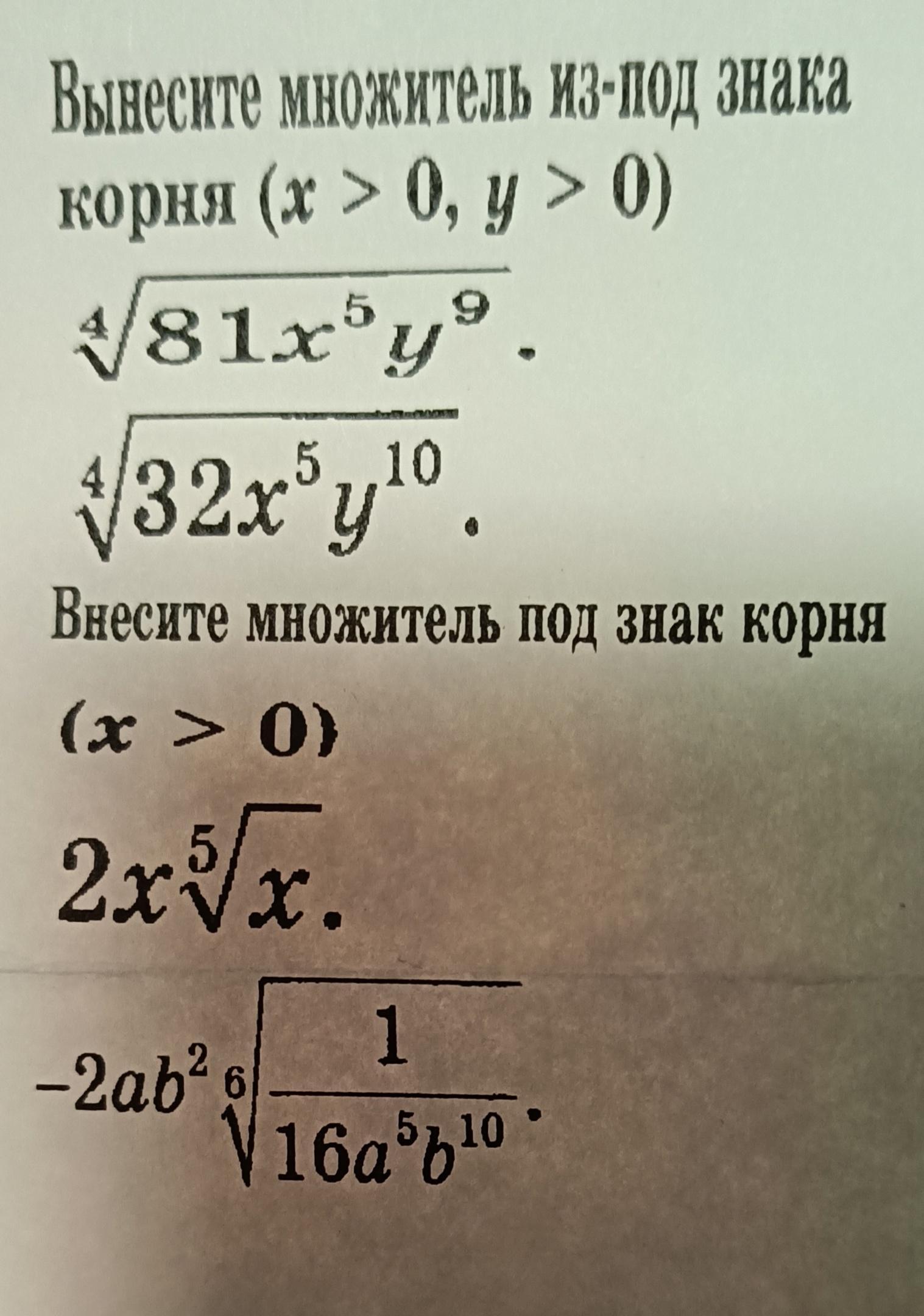
Ответы на вопрос
Ответил natalyabryukhova
1
Ответ:
Объяснение:
Вынесите множитель из под знака корня:
(x > 0, y > 0)
1.
- Произведение двух степеней с одинаковыми основаниями равно степени с тем же основанием и показателем, равным сумме показателей множителей:
- Для любых действительных чисел a и b таких, что a ≥0 и b≥0 выполняется равенство:
- Для любого действительного числа a и любого натурального числа n выполняется равенство:
- Модуль положительного числа - само это число.
2.
Внесите множитель под знак корня.
1. , x > 0
Свойства корней:
2.
Дан корень четной степени, следовательно, подкоренное выражение неотрицательно.
Так как b¹⁰ > 0 ⇒ a⁵ > 0 или a > 0
- Под корень четной степени можем вносить только положительные числа.
#SPJ1
Новые вопросы
Математика,
4 месяца назад
Физика,
4 месяца назад
Математика,
6 месяцев назад
Другие предметы,
6 месяцев назад
Английский язык,
6 лет назад