Алгебра, вопрос задал a5ttt , 7 лет назад

ПОМОГИТЕ ПОЖАЛУЙСТА ,решить уравнение

Приложения:

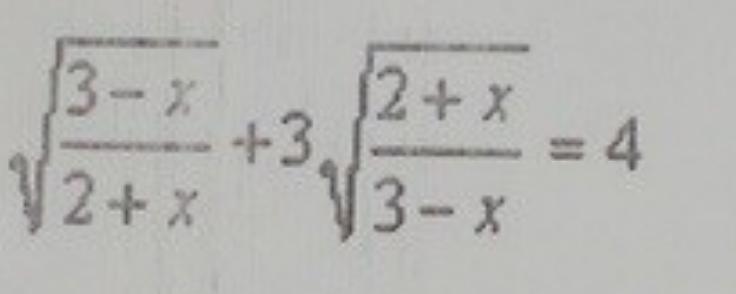
Ответы на вопрос

Ответил valenivan

Решение задания приложено

Если без ОДЗ, то проверка обязательна.

Приложения:

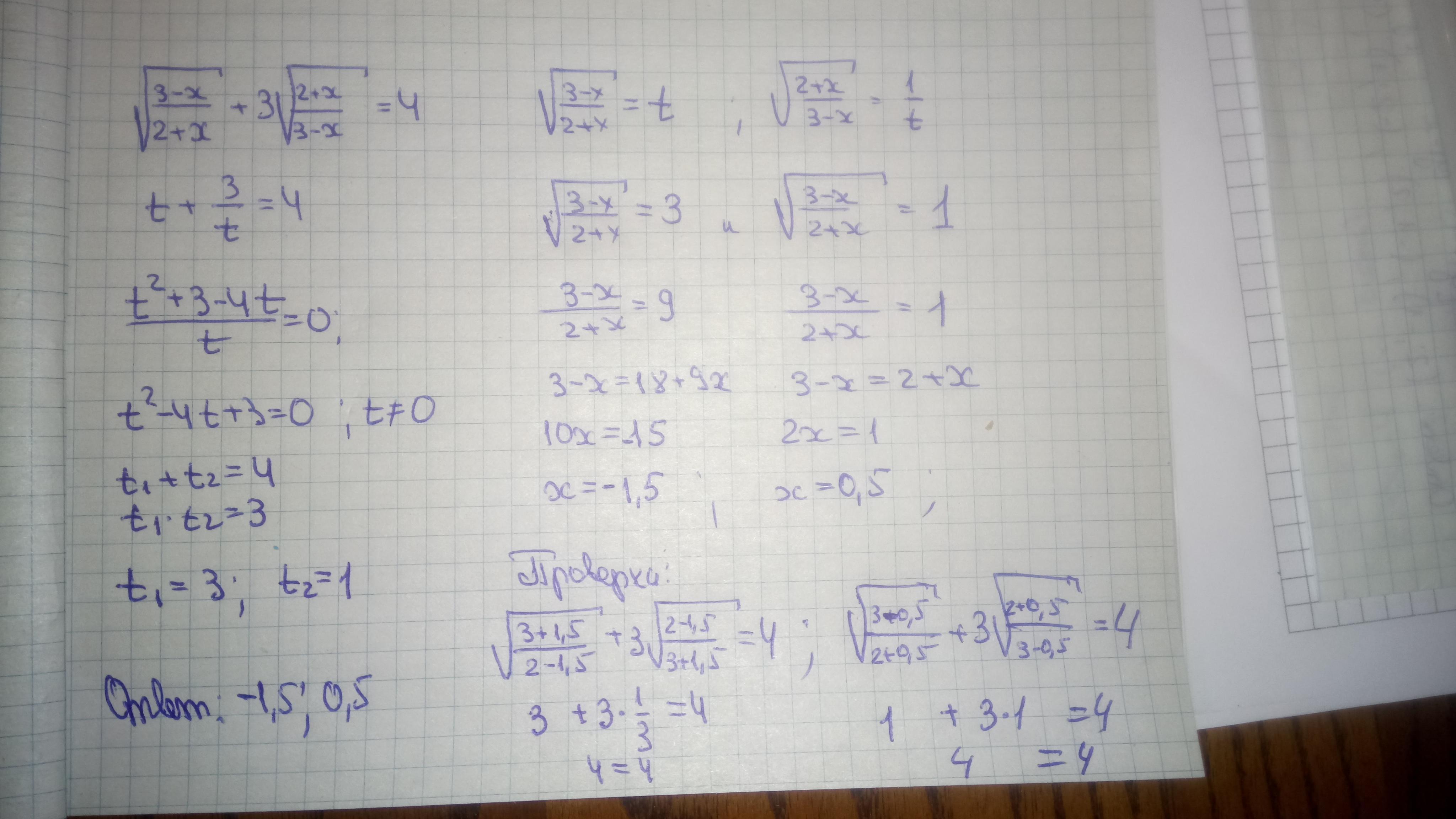
Ответил a5ttt

это точно правильно?

Ответил Аноним

Да, точно.

Ответил a5ttt

спасибо)

Ответил valenivan

Если проверка показала, что корни найдены верно, то решение верно. Оно может двумя способами. Второй вам предоставили.

Ответил Аноним

$sqrt{frac{3-x}{2+x}} + 3sqrt{frac{2+x}{3-x}} = 4$

Введём замену: t = $frac{3-x}{2+x}$

$sqrt{t} + 3sqrt{frac{1}{t}} = 4$

Возведём обе части уравнения в квадрат:

$t + 6 + frac{9}{t} = 16\t + 6 + frac{9}{t} - 16 = 0\t - 10 + frac{9}{t} = 0$

Приводим к одному знаменателю:

$frac{t^{2} - 10t + 9}{t} = 0\tneq 0\t^{2} - 10t + 9 = 0\\left {{t_{1}{t_{2} = 9} atop {{t_{1} +{t_{2} = 10} right.\\t = 1\t = 9$

По теореме Виета найдены два корня уравнения.

Вернёмся к исходной переменной:

$frac{3-x}{2+x} = 1$

$frac{3-x}{2+x} = 9$

Решаем два последних уравнения.

$frac{3-x}{2+x} = 1\ 3-x = 2+x\- x - x = 2 -3\-2x = -1\x = 0,5\\\frac{3-x}{2+x} = 9\3-x = 9(2+x)\3-x = 18+9x\-x-9x = 18 -3\-10x = 15\x = -1,5$

Уравнение решено.

Ответ: x = 0,5; x = -1,5.

Приложения:

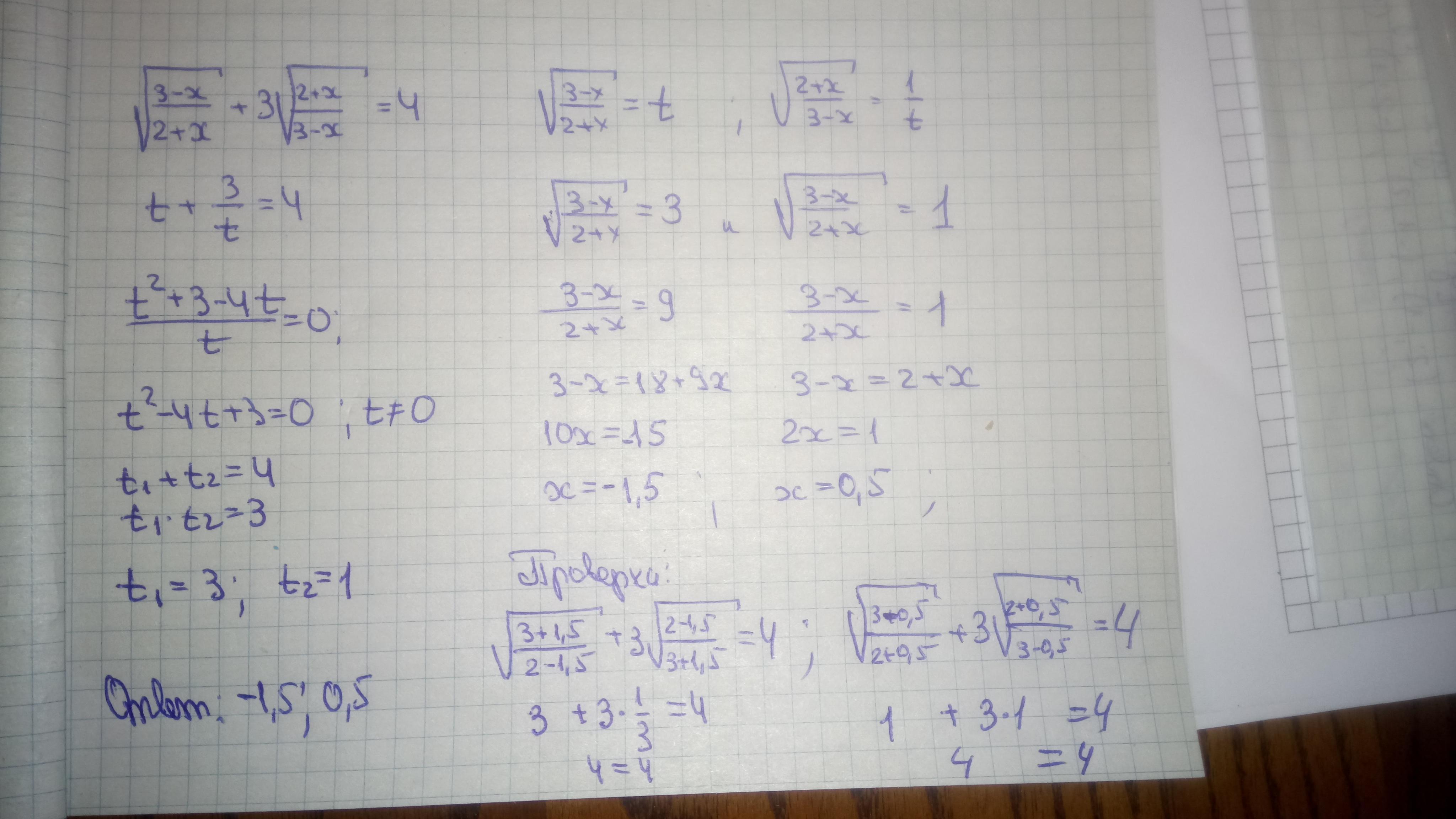
Ответил a5ttt

спасибо)

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Русский язык, 1 год назад

А17. Найдите производный предлог. 1) около дома; 2) вместо товарища; 3) на том берегу; 4) из-за болезни. А18. Найдите производный предлог, пишущийся слитно. 1) (в)виду дождя; 2) (в)продолжение года;...

Русский язык, 1 год назад

глухие согласные в корне слово 10 слов помогите плизз...

Физика, 7 лет назад

Физика: скорость движения велосипедиста 8 км ч. Какой путь он проедет за 1 ч 15 мин?

География, 7 лет назад

Какой из этих напитков происходит из Африки?А.чай.Б.какао.В.кофе;Г.квас;Д;кефир.

География, 8 лет назад

Определите летнее время в Якутске, в Магадане, если в Москве 10 часов утра?

История, 8 лет назад

Помогите пожалуста придумать фантастический рассказ.. типа описать что увидела бы если оказалась в древнем мире. Задание по истории, а фантазии 0. Заранее спасибо!