Алгебра, вопрос задал Кариночка78 , 7 лет назад

Помогите, пожалуйста, решить тригонометрическое уравнение. Подробно

Приложения:

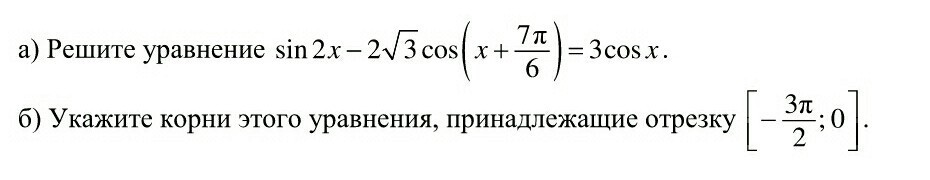
Ответы на вопрос

Ответил Artem112

$sin2x-2 sqrt{3} cosleft(x+ dfrac{7 pi }{6} right)=3cos x$
$sin2x-2 sqrt{3} left(cos xcos dfrac{7 pi }{6} -sin xsin dfrac{7 pi }{6} right)=3cos x$
$sin2x-2 sqrt{3} left(cos xcdotleft(- dfrac{ sqrt{3} }{2}right) -sin xcdotleft(- dfrac{ 1 }{2}right) right)=3cos x$
$sin2x-2 sqrt{3} left(-dfrac{ sqrt{3} }{2} cos x+ dfrac{ 1 }{2}sin x right)=3cos x$
$sin2x+3cos x- sqrt{3} sin x =3cos x$
$sin2x- sqrt{3} sin x =0$
$2sin xcos x- sqrt{3} sin x =0$
$sin xleft(2cos x- sqrt{3}right) =0 \ sin x=0Rightarrow boxed{x_1= pi n , nin Z} \ 2cos x- sqrt{3}=0Rightarrow cos x= dfrac{ sqrt{3} }{2} Rightarrow boxed{x_2=pm dfrac{ pi }{6} +2 pi n, nin Z}$

Отбор корней.
1 серия:
$- dfrac{3 pi }{2} leq pi n leq 0$
$- dfrac{3 }{2} leq n leq 0$
$n=0: boxed{x=0}$
$n=-1: boxed{x=- pi }$
2 серия:
$- dfrac{3 pi }{2} leq dfrac{ pi }{6} +2 pi n leq 0$
$- dfrac{3 }{2} leq dfrac{1 }{6} +2 n leq 0$
$- dfrac{3 }{2}-dfrac{1 }{6} leq 2 n leq -dfrac{1 }{6}$
$- dfrac{5 }{4} leq 2 n leq -dfrac{1 }{6}$
$- dfrac{5 }{8} leq n leq -dfrac{1 }{12}$
$nnotin Z$
3 серия:
$- dfrac{3 pi }{2} leq -dfrac{ pi }{6} +2 pi n leq 0$
$- dfrac{3 }{2} leq- dfrac{1 }{6} +2 n leq 0$
$- dfrac{3 }{2}+dfrac{1 }{6} leq 2 n leq dfrac{1 }{6}$
$- dfrac{4 }{3} leq 2 n leq dfrac{1 }{6}$
$- dfrac{2 }{3} leq n leq dfrac{1 }{12}$
$n=0: boxed{x=-dfrac{ pi }{6}}$

Ответил m11m

Есть ещё один корень. В первой серии: n= -1 x= - pi

Ответил Artem112

Спасибо

Предыдущий вопрос

Следующий вопрос

Новые вопросы

История, 1 год назад

Украйна у другій Світовій війні Коли почалась і скільки тривала операція німецького командування по окупації України? Скiльки тривала оборона нашого міста? Хто нею керував Чи був здійснений...

Информатика, 1 год назад

Лука в кинотеатре Ограничение по времени: 1 секунда Воскресным утром в кинотеатре в двух залах одновременно начался показ фильмов. Фильм, показываемый в первом зале, имеет длительность a минут, а...

Математика, 7 лет назад

помогите пожалуйста задать вопрос из двух городов навстречу друг другу ваехали два велосипидиста и встретились через 4 часа.Скорость одного велосипидиста 15км/ч, а скорость другого 10км/ч...

История, 7 лет назад

1. Укажите год, когда окончились события, обозначенные на схеме. 2. Укажите название полуострова, захват которого отображен на схеме. 3.Напишите фамилию главнокомандующего белогвардейскими...

Алгебра, 8 лет назад

Вычислить путь,прлходимый точкой со скоростью U=3t+1 (м/с) при t1= 2c; t2=4c (Полное решение )...

Математика, 8 лет назад

Решить всё соревнований два спортсмена стартовали в 11 ч 06 мин. Один из них пробежал дистанцию за 1мин 57 с , а с другой пришёл к финишу на 5 с позже. Какое время показывал секундомер , когда...