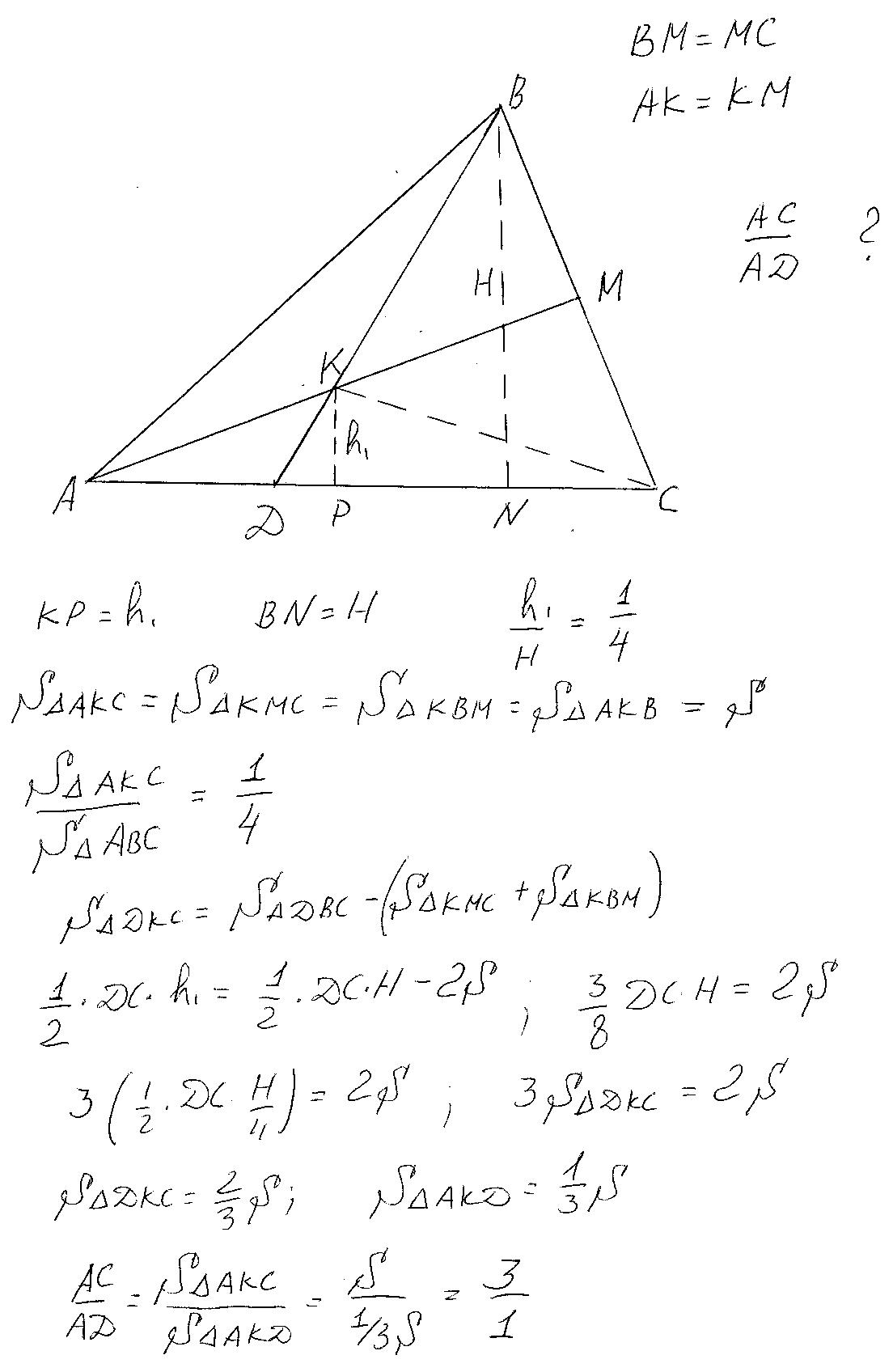
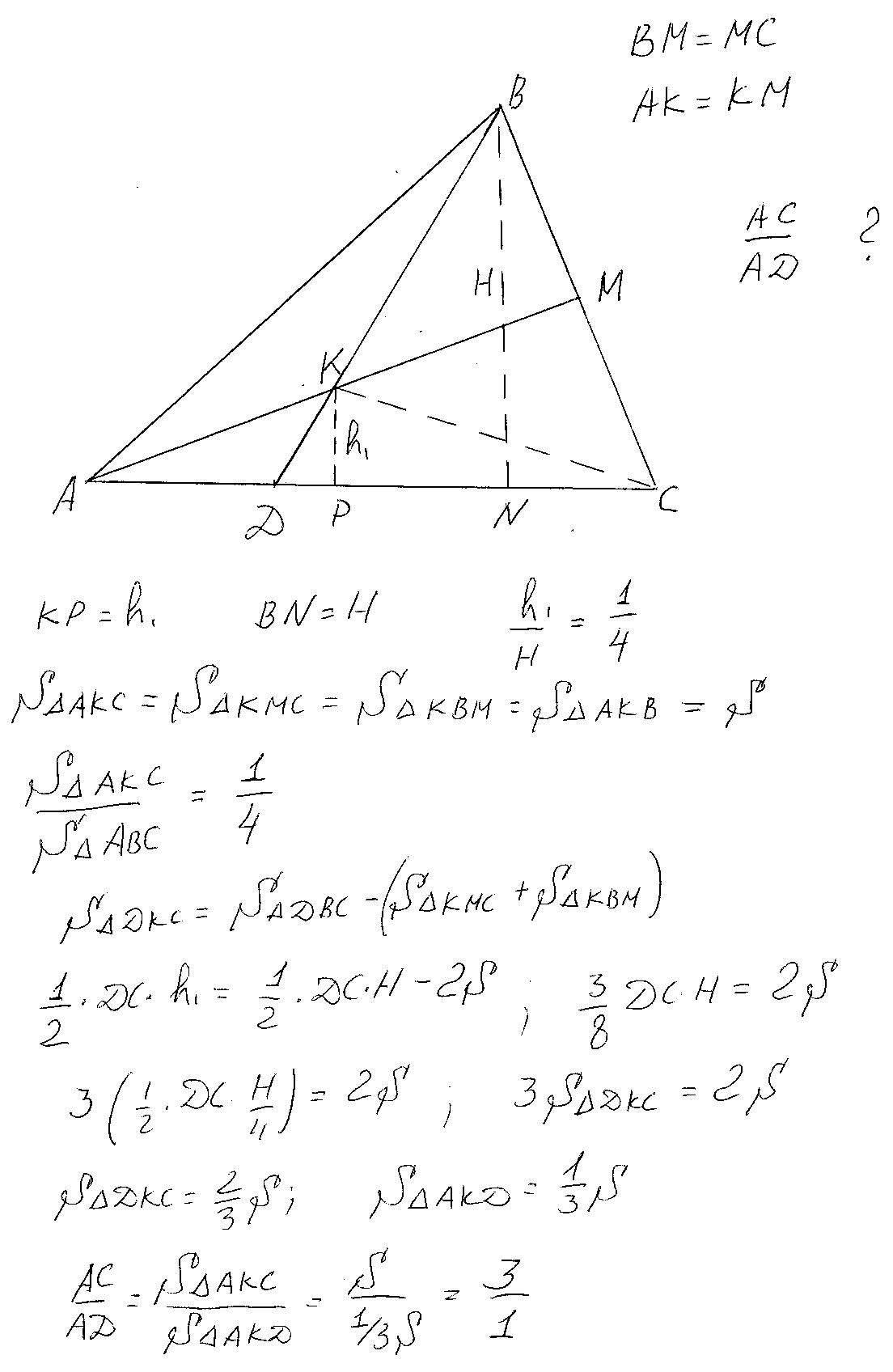
Помогите пожалуйста решить: Точка К - середина медианы AM треугольника ABC, прямая BK пересекает сторону AC в точке D. Найдите отношение AC:AD
Ответы на вопрос
Ответил Fatter
0
Площади треугольников АКС , КМС, КВМ, АКВ равны. Поскольку они попарно равны при рассмотрении треугольников АМС, ВКС и АВМ у которых соответственно КС, КМ и ВК медианы. То есть получается, что треугольник АВС состоит из четырёх равных треугольников.Пусть площадь каждого равна S. У треугольников АВС и АКС общее основание , следовательно отношение их высот будет равно отношению площадей(смотри рисунок). Далее находим площадь треугольника ДКС через S. И окончательно АС/АД=3/1.
Приложения:
Новые вопросы
Физика,
6 лет назад
Литература,
6 лет назад
Литература,
9 лет назад
Алгебра,
9 лет назад
Математика,
10 лет назад