Помогите пожалуйста решить предел функции :(
Приложения:
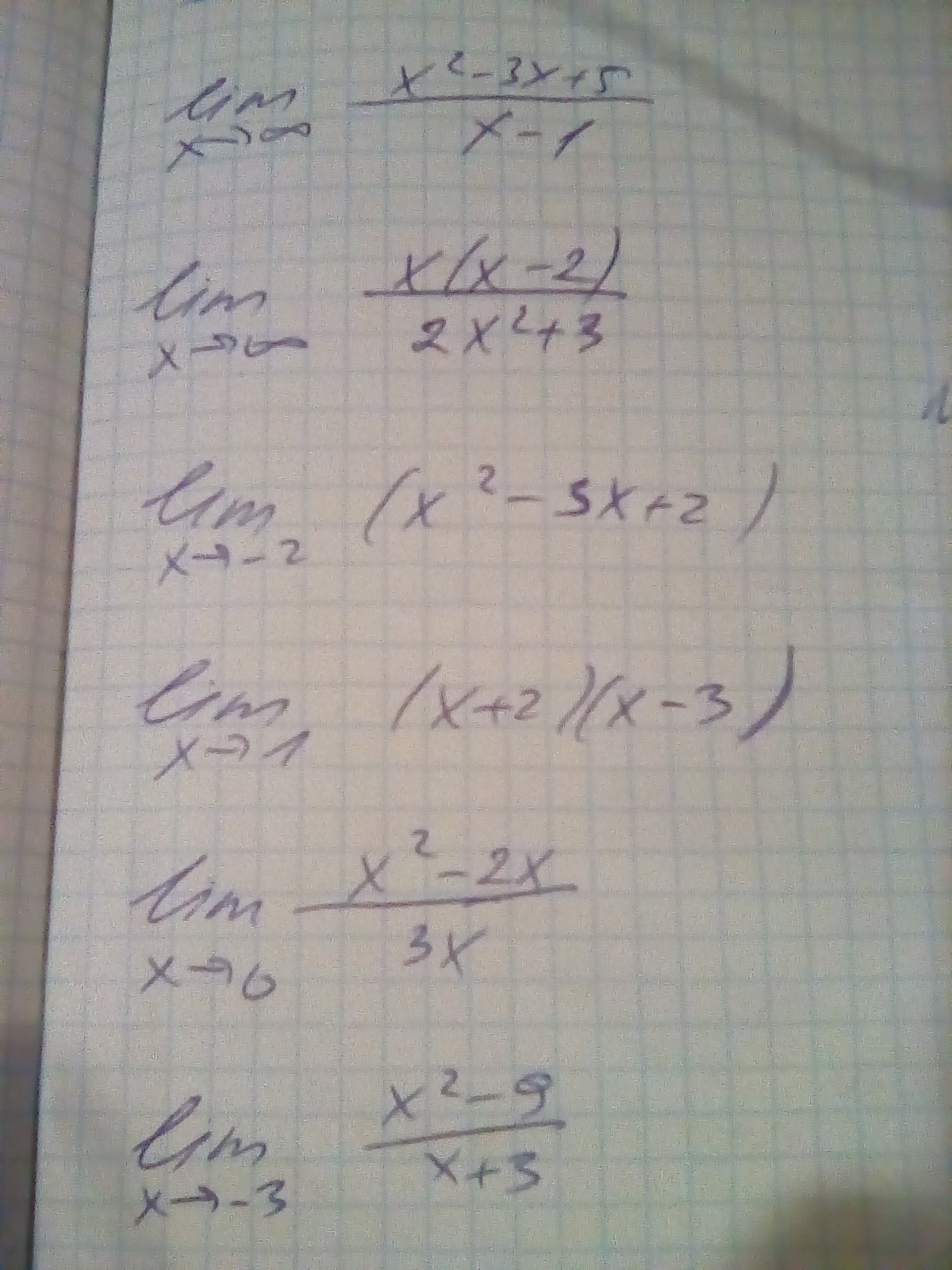
Сабрина88:
Заранее благодарю
Ответы на вопрос
Ответил Удачник66
0
1) Делим числитель и знаменатель на старшую степень x^2

2) Тоже самое

3) Просто подставляем число в выражение

4) Тоже самое

5) Сокращаем x

6) Разложим числитель на множители и сократим

2) Тоже самое
3) Просто подставляем число в выражение
4) Тоже самое
5) Сокращаем x
6) Разложим числитель на множители и сократим
Новые вопросы