Помогите пожалуйста решить методом Гаусса, 3 способами
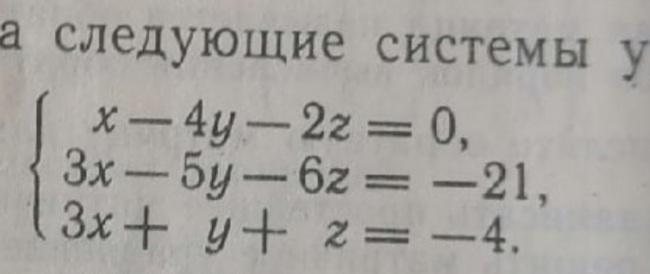
Ответы на вопрос
запишем расширенную матритцу
1 -4 -2 0
3 -5 -6 -21
3 1 1 -4
умножим первую строку на -3 и сложим со второй, потом с третьей, получим
1 -4 -2 0
0 7 0 -21
0 13 7 -4
разделим вторую строку на 7
1 -4 -2 0
0 1 0 -3
0 13 7 -4
умножим вторую на -13 и сложим с третьей
1 -4 -2 0
0 1 0 -3
0 0 7 35
из последнего уравнения 7z=35; z=5; из второго у=-3, подставим найденное в первое уравнение. получим х=4у+2z=-12+10=-2
Ответ х=-2; у=-3; z=5
2 способ метод Крамера
находим определители
Δ=
1 -4 -2
3 -5 -6
3 1 1=
-5+72-30-6+6+12=49
Δ₁=
0 -4 -2
-21 -5 -6
-4 1 1=
-96+42+40-84=-98
Δ₂=
1 0 -2
3 -21 -6
3 -4 1=
-21+24-24-126=-147
Δ₃=
1 -4 0
3 -5 -21
3 1 -4=
20+252-48+21=245
x=-98/49=-2
y=-147/49=-3
z=2454/49=5
3 способ обратной матрицы
Найдем алгебраические дополнения.
А₁₁=-5+6=1
А₁₂=-(3+18)=-21
А₁₃=3+15=18
А₂₁=-(-4+2)=2
А₂₂=1+6=7
А₂₃=-(1+12)=-13
А₃₁=24-10=14
А₃₂=-(-6+6)=0
А₃₃=-5+12=7
обратная матрица
1/ 49 2/49 14/49
-21/49 7/49 0
18/49 -13/49 7/49
умножим на вектор - столбец свободных членов
0
-21
-4
получим х=(0-42-56)/49=-2
у=(0-147+0)/49=-3
z=(0-21*(-13)-28)/49=(2734-28)/49=5
ОТВЕТ ВЕЗДЕ ОДИНАКОВ.
Х=-2
У=-3
Z=5