Помогите пожалуйста решить логарифмическое уравнение (6)
Приложения:
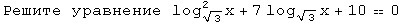
Ответы на вопрос
Ответил ShirokovP
0
Ответил dnepr1
0
Дано уравнение 
Введём замену:
Получаем квадратное уравнение:

Квадратное уравнение, решаем относительно t: Ищем дискриминант:
D=7^2-4*1*10=49-4*10=49-40=9;Дискриминант больше 0, уравнение имеет 2 корня: t₁=(√9 -7)/(2*1)=(3-7)/2=-4/2=-2; t₂=(-√9-7)/(2*1)=(-3-7)/2=-10/2=-5.
Производим обратную замену:


Введём замену:
Получаем квадратное уравнение:
Квадратное уравнение, решаем относительно t: Ищем дискриминант:
D=7^2-4*1*10=49-4*10=49-40=9;Дискриминант больше 0, уравнение имеет 2 корня: t₁=(√9 -7)/(2*1)=(3-7)/2=-4/2=-2; t₂=(-√9-7)/(2*1)=(-3-7)/2=-10/2=-5.
Производим обратную замену:
Приложения:
Новые вопросы