Помогите пожалуйста решить две задачи по геометрии, буду очень благодарна, кто решит правильно. Как всегда, оформлять дано и решение, грамотно и правильно! ДАЮ 20 БАЛЛОВ, задачи в файле!

Ответы на вопрос
Ответ:
1) Стороны треугольника равны:
или
2) Стороны треугольника: ВС = 3 см; АВ = 6 см; АС = 1 см.
Треугольника со сторонами 3 см, 6 см, 1 см не существует.
Объяснение:
1) Найти стороны треугольника (рассмотреть все варианты).
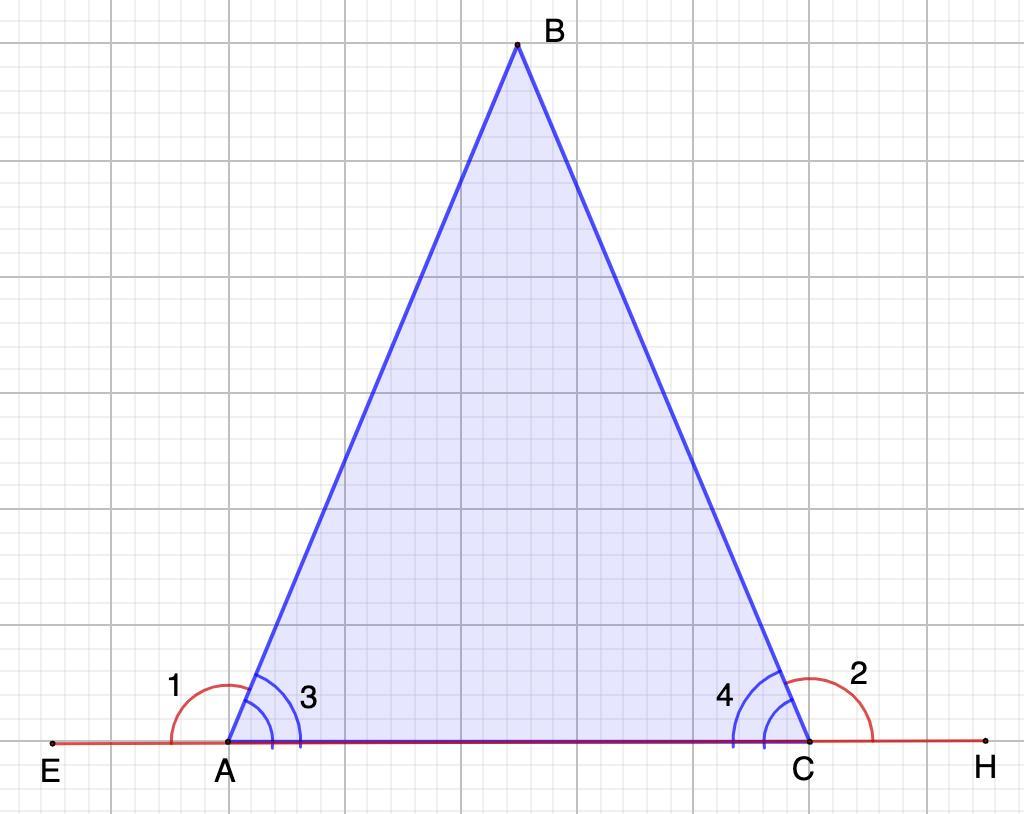
Дано: ΔАВС.
∠1 = ∠2 - внешние.
Р (АВС) = 60 см;
Одна сторона больше другой на 10 см.
Найти: стороны треугольника.
Решение:
1. ∠1 = ∠2 - внешние.
- Смежные углы в сумме составляют 180°.
⇒ ∠3 = 180° - ∠1 (смежные)
∠4 = 180° - ∠2 (смежные)
---------------------------
⇒ ∠3 = ∠4
2. Рассмотрим ΔАВС.
∠3 = ∠4
- Если в треугольнике два угла равны, то этот треугольник равнобедренный.
⇒ ΔАВС - равнобедренный.
АВ = ВС
3. Пусть АС = х см, тогда АВ = ВС = (х + 10) см
- Периметр - сумма длин всех сторон треугольника.
Р (АВС) = АС + АВ + ВС = 60 см
х + х + 10 + х + 10 = 60
3х = 40
Стороны треугольника равны:
4. Рассмотрим второй случай.
Пусть АВ = ВС = х см, тогда АС = (х + 10) см
Р (АВС) = АВ + ВС + АС
х + х + х + 10 = 60
3х = 50
Стороны треугольника равны:
2) Найти стороны треугольника.
Дано: ΔАВС;
Первая сторона АВ- ?;
Вторая сторона ВС - ? в два раза меньше первой;
Третья сторона АС - ? на 5 см меньше первой.
Р (АВС) = 10 см.
Найти: стороны треугольника.
Решение:
Пусть ВС = х см, тогда АВ = 2х см, а АС = (2х - 5) см.
Р (АВС) = 10 см.
Р (АВС) = АВ + ВС + АС
х + 2х + 2х - 5 = 10
5х = 15
х = 3
Получили стороны треугольника:
ВС = 3 см; АВ = 6 см; АС = 1 см.
Проверим, существует ли такой треугольник?
- Для любого треугольника сумма длин любых двух сторон должна быть больше длины третьей стороны.
Сравним:
ВС + АС и АВ
3 + 1 < 6 или 4 см < 6 см
⇒ Треугольника со сторонами 3 см, 6 см, 1 см не существует.