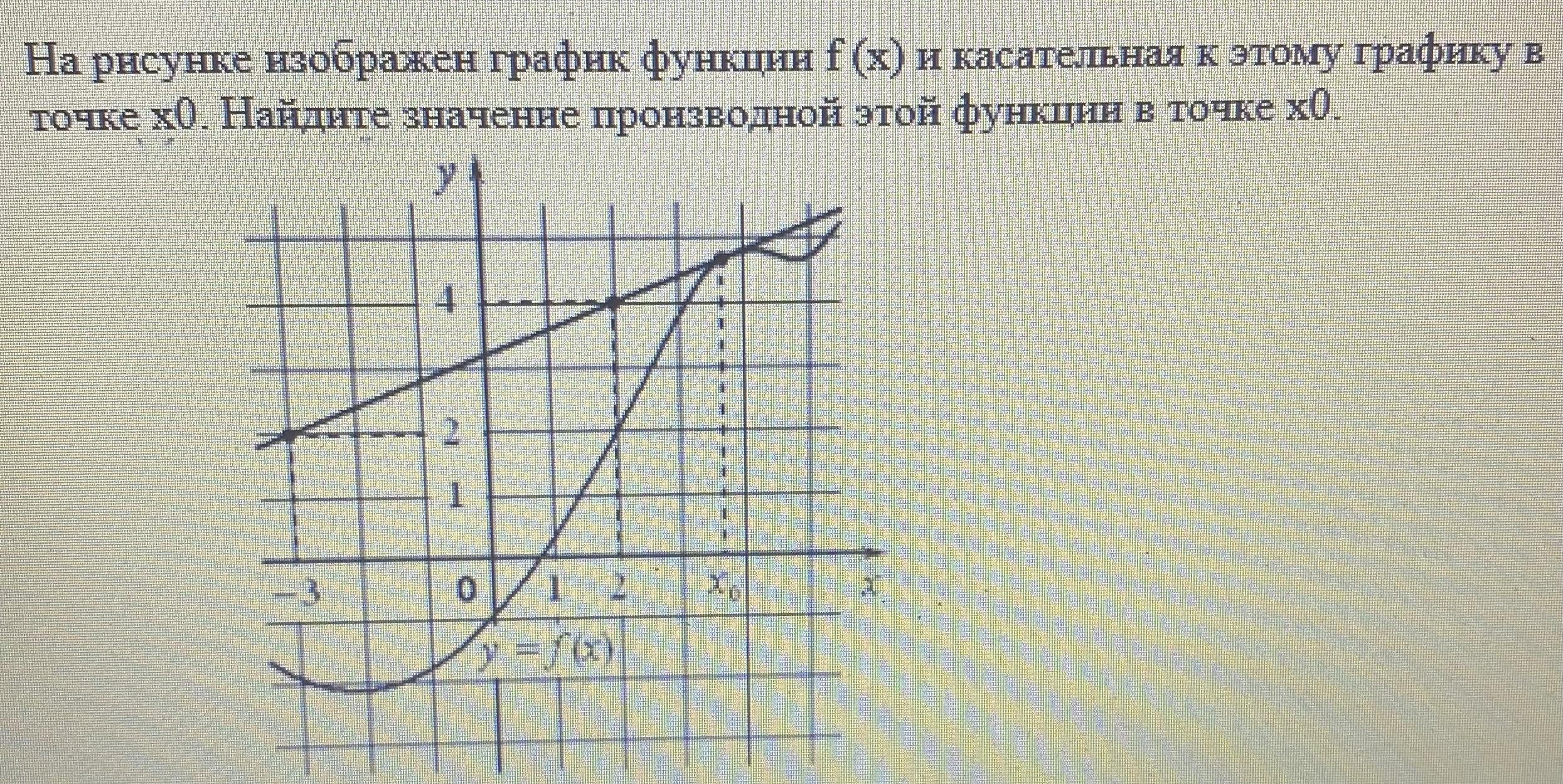
Помогите пожалуйста решить

Ответ:    .

Значение производной функции в точке равно угловому коэффициенту касательной в этой точке .  

Угловой коэффициент касательной в точке равен  тангенсу угла наклона касательной к положительному направлению оси ОХ.

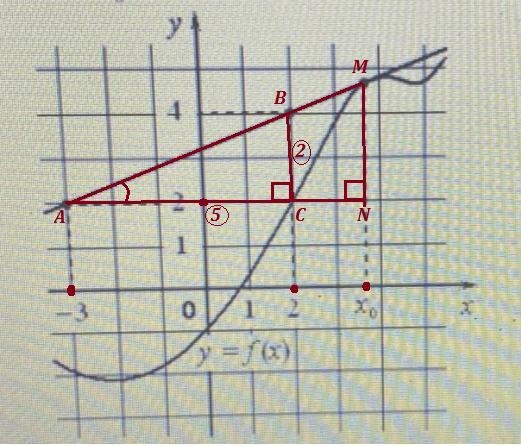
Найдём его из прямоугольного  треугольника AMN  как tg∠MAN .

Но ΔAMN подобен ΔАВС , так как MN || ВС, и  ∠MAN =∠ВАС . А найти тангенс ∠ВАС легко, так как точки В, С и А являются узловыми .

tg∠ВAC =ВС/АС  = 2/5  .

Значит,    .