Помогите пожалуйста решить
Приложения:
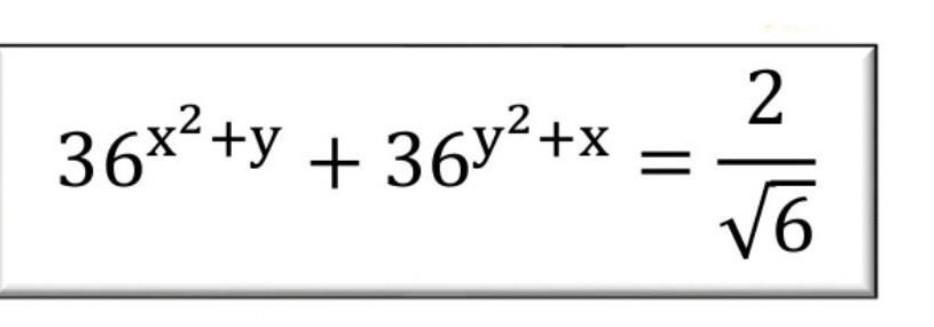
bb573878:
если можно, что именно нужно найти?
х=у= -½
Ответы на вопрос
Ответил yugolovin
5
По неравенству Коши между средними арифметическим и средним геометрическим двух положительных чисел мы имеем
Мы доказали, что левая часть уравнения всегда больше или равна правой. Чтобы левая и правая части были равны, нужно, чтобы все неравенства в нашей цепочке были равенствами. Первое становится равенством, когда a=b - это входит в формулировку неравенства Коши, - в нашем случае когда
Второе неравенство становится равенством, когда x=-1/2; y=-1/2.
Видим, что при таких x и y первое неравенство также превращается в равенство, поэтому найденные x и y дают ответ.
Ответ: ( - 1/2: - 1/2).
красивое решение
помогите и мне пожалуйста, очень прошу
Новые вопросы
Математика,
1 год назад
Қазақ тiлi,
1 год назад
Математика,
6 лет назад
Математика,
6 лет назад
Математика,
8 лет назад
Литература,
8 лет назад