Помогите пожалуйста. Пример по теме "Сочетания без повторений и бином Ньютона". Никак не могу понять как и по какой формуле это найти((
Приложения:
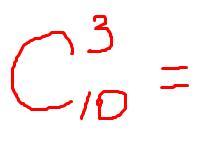
Ответы на вопрос
Ответил mic61
1
Ответ:
120
Объяснение:
Элементы комбинаторики.
С - это число сочетаний из десяти по три.
Сколькими способами можно выбрать три элемента множества, если множество состоит из десяти элементов? При этом не учитывется в каком порядке выбираются эти три элемента.
Пусть есть множество из 10 натуральных чисел:
{1, 2, 3..., 10}
Выбираем произвольно 3-и элемента. Например
{1, 2, 3}
Сколько таких выборок можно сделать? При условии, что выборки {1, 2, 3} {2, 1, 3} и т.д. - считаются одной и той же выборкой (порядок не учитывается!)
Вобщем формула давно выведена, и для данного случая выглядит так:
С_10_3=(10!)/[(10-3)!*3!]
10! - читается "десять факториал"
10!=1*2*3*...*9*10.
значит:
С_10_3=(10!)/[(10-3)!*3!] = (10!)/[7!*3!]=8*9*10/(1*2*3)=720/6=120
Новые вопросы