Геометрия, вопрос задал shiftyqbz , 1 год назад

Помогите пожалуйста по геометрии.
Условие в 6 задаче: треугольник правильный

Приложения:

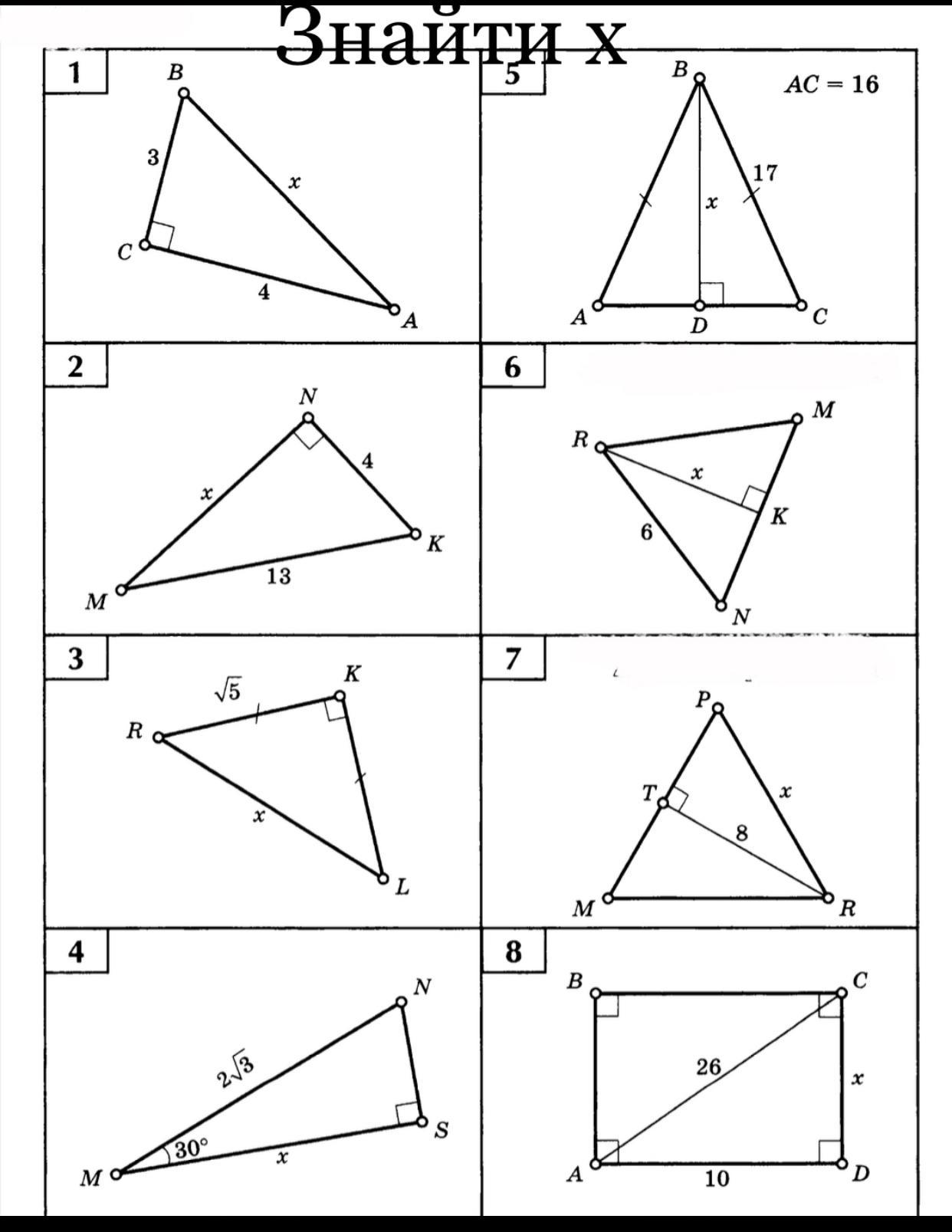
Ответы на вопрос

Ответил Ameba1kletochnaya

Ответ:

смотри, на 8 фотках можно заюзать теорему Пифагора, т.к. треугольники прямоугольные, которые надо рассмотреть. чтоб не расписывать, напишу сразу как она читается: квадрат гипотенузы = суме квадратов катетов. а чтоб избавится от квадрата подносим к корню. допустим а, b - катеты, с - гипотенуза. тогда формула будет такого вида: $c = \sqrt{a^{2} +b^{2} }$ , $a = \sqrt{c^{2} -b^{2} }$ , $b = \sqrt{c^{2} -a^{2} }$ . теперь сугубо по тем формулам

1) х = $\sqrt{16+9} = 5$ см

2) х = $\sqrt{169 - 16} = \sqrt{153}$ см

3) треугольник равнобедренный прямоугольный, у такого гипотенуза на $\sqrt{2}$ см больше за катет, то есть х = $\sqrt{5} * \sqrt{2} = \sqrt{10}$ см

4) катет, что лежит против угла 30 градусов, это NS , = половине гипотенузы = $\frac{2\sqrt{3} }{2}$ = $\sqrt{3}$ см. за теоремой Пифагора х = $\sqrt{(2\sqrt{3} )^{2} - \sqrt{3}^{2}} =\sqrt{4*3-3} =\sqrt{12-3} =\sqrt{9} = 3$ см

5) треугольник равнобедренный, значит высота RD, проведенная к основанию, есть сразу и медиана, и бисектриса. в таком случае треугольник RDC - прямоугольный равнобедреный, тогда теорема Пифагора будет такая: $x^{2} +x^{2} = 17$

$2x^{2} = 289$

$x^{2} = 144,5$

х= $\sqrt{144,5}$ ≈ 12 см

6) так как треугольник правильный, то все стороны равны. в таком случае треугольник RКМ - прямоугольный равнобедреный, тогда теорема Пифагора будет такая: $x^{2} +x^{2} = 36$

$2x^{2} =36$

$x^{2} =18$

х= $\sqrt{18}$

х= $\sqrt{9*2}$

х= $3\sqrt{2}$ см

7) треугольник РТR - прямоугольный равнобедреный, тогда теорема Пифагора будет такая: $x =\sqrt{64+64}$ = $\sqrt{128}$ = $\sqrt{2*64}$ = $8\sqrt{2}$ см

8) так как АС - диагональ, она делит углы на 2 равных, тоесть по 45 градусов, в таком случае треугольник АDC - прямоугольный равнобедреный, тогда теорема Пифагора будет такая: х = $\sqrt{26^{2} - 100}$ = $\sqrt{676 - 100} = \sqrt{576} = 24$ см