Математика, вопрос задал Каролина09 , 7 лет назад

Помогите пожалуйста
Нужно найти общее решение дифференциального уравнения первого порядка

Приложения:

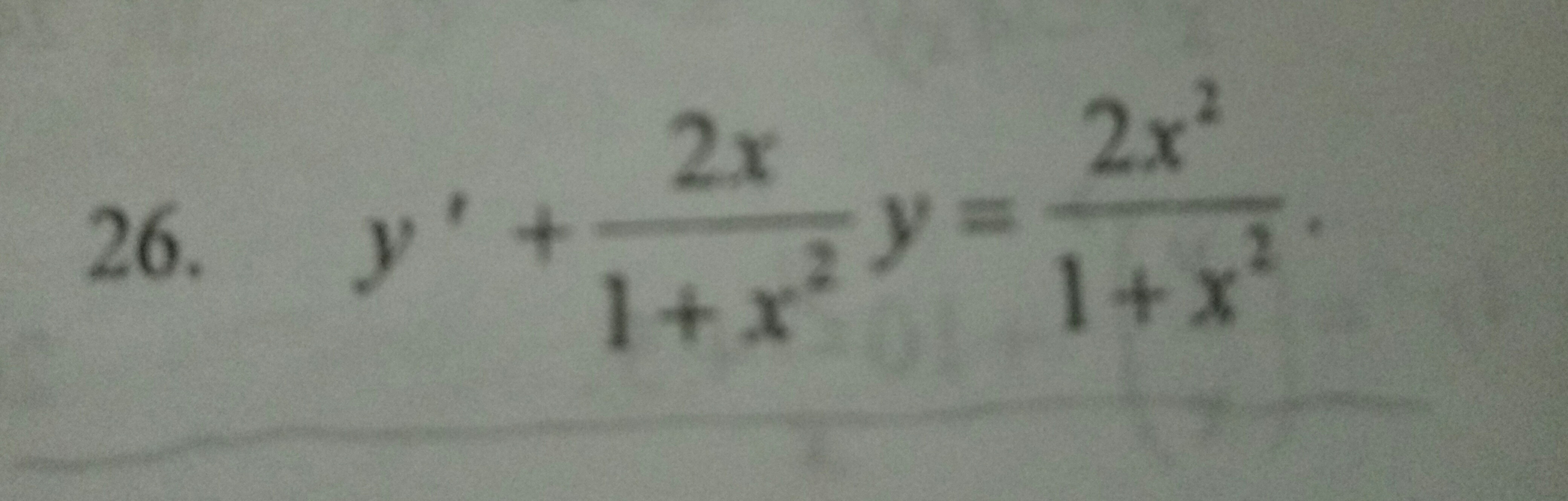
Ответы на вопрос

Ответил Alexandr130398
0
уравнение вида:
y'+P(x)y=Q(x)
Называется линейным неоднородным дифференциальным уравнением первого порядка (или частным случаем уравнения Бернулли)
Такие уравнения решаются либо методом вариации постоянной, либо методом Бернулли. Я покажу второй метод

Решение:
y'+ frac{2x}{1+x^2} y= frac{2x^2}{1+x^2} \ \

Замена: y=uv;  y'=u'v+v'u, тогда

u'v+v'u+ frac{2x}{1+x^2} uv= frac{2x^2}{1+x^2} \ \ u'v+u(v'+ frac{2x}{1+x^2}v)=frac{2x^2}{1+x^2} \ \ v'+ frac{2x}{1+x^2}v=0 \ \ frac{dv}{dx} + frac{2x}{1+x^2}v=0 \ \ frac{dv}{dx} =- frac{2x}{1+x^2}v \ \ frac{dv}{v} =- frac{2x}{1+x^2}dx

intlimits {frac{dv}{v}}=- intlimits {frac{2x}{1+x^2} } , dx \ \ ln|v|=- intlimits {frac{1}{1+x^2} } , d(1+x^2) \ \ ln|v|=-ln|1+x^2| \ \ ln|v|=ln | frac{1}{1+x^2} | \ \ v= frac{1}{1+x^2}

u'v+u(v'+ frac{2x}{1+x^2}v)=frac{2x^2}{1+x^2}
Так как выражения в скобках приравнивалось к нулю, то остается:

u'v=frac{2x^2}{1+x^2}

подставляем значение v:

u'frac{1}{1+x^2}=frac{2x^2}{1+x^2} |*(1+x^2) \ \ u'=2x^2 \ \ u= intlimits {2x^2} , dx = frac{2x^3}{3} +C

И наконец, обратная замена:

y=uv=(frac{2x^3}{3} +C)* frac{1}{1+x^2} \ \ OTBET: y=(frac{2x^3}{3} +C) frac{1}{1+x^2}
Предыдущий вопрос
Следующий вопрос
Новые вопросы
Русский язык, 1 год назад
Напиши небольшое описание пейзажа за окном школы или дома. Помогите, срочно нужно!
Русский язык, 1 год назад
какими звуками различается каждая пара слов? произнесите эти звуки (капли-цапля лук-люк хор-хорь)...
Математика, 7 лет назад
Решить уравнение Решить уравнение 4х - 2 = х СРОЧНО!!!!!!!!!!!!!!
Химия, 7 лет назад
Дать определение кислотам с точки зрения теории электролитической диссоциации. Написать уравнения диссоциации следующих веществ: H3PO4; HCL; H2SO4; NaNO3; NH4OH; BaBr2 и укажите класс соединений. дам...
Математика, 8 лет назад
Около прямоугольного треугольника ABC с прямым углом С=90 градусов описана окружность.Найти радиус этой окружности,если AC=8см,Bc=6см...
Математика, 8 лет назад
1 целаю 5/6х- 2/3х+0,25 при х=6...