Математика, вопрос задал Санечка99 , 7 лет назад

Помогите пожалуйста, не понимаю эту тему. С объяснением если можно)))

Приложения:

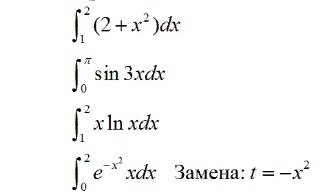
Ответы на вопрос

Ответил artalex74

$int limits_{1}^{2} (2+x^2)dx = (2x+ frac{x^3}{3} ) big | _{1}^{2} = (4+ frac{8}{3} )-(2+ frac{1}{3})=2+ frac{7}{3}=2 frac{1}{3}$

$int limits_{0}^{ pi } sin 3x dx =(- frac{1}{3} cos 3x) big | _{0}^{ pi } = -frac{1}{3}(cos 3 pi - cos 0 )=-frac{1}{3}*(-1-1) = frac{2}{3}$

$int limits_{1}^{2} x ln x dx = frac{1}{2} int limits_{1}^{2} ln x d(x^2) = frac{1}{2} (x^2 ln x) big | _{1}^{2} - frac{1}{2} int limits_{1}^{2} x^2 d( ln x ) =\ = frac{1}{2} (4 ln 2 - ln 1) - frac{1}{2} int limits_{1}^{2} x dx = 2ln 2 - frac{x^2}{4} big | _{1}^{2} = 2ln 2 - (1-frac{1}{4}) =\ = 2ln 2 -frac{3}{4}$

$int limits_{0}^{2} e^{-x^2} x dx = - frac{1}{2} int limits_{0}^{2} e^{-x^2}d(-x^2) = Big [ t= -x^2 Big ] = - frac{1}{2} int limits_{0}^{-4} e^tdt = \ = frac{1}{2} int limits_{-4}^{0} e^tdt = frac{1}{2} e^t big | _{-4}^{0} = frac{1}{2} (1-e^{-4}})$

Приложения:

Предыдущий вопрос

Следующий вопрос

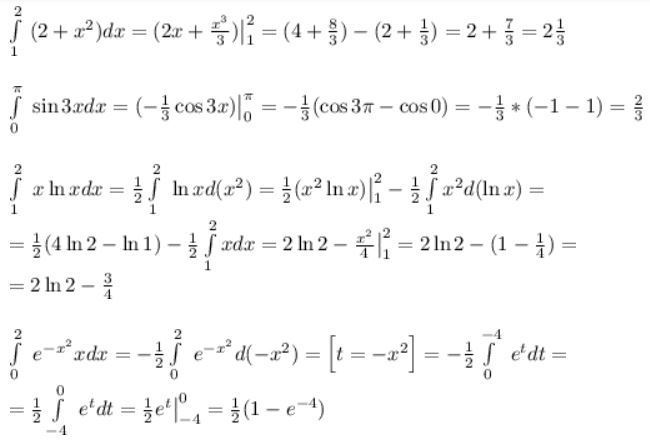
Новые вопросы

Алгебра, 1 год назад

Представьте в виде произведения: а) (х – 4)2 – 25х2; б) а2 – b2 – 4b – 4а.

Английский язык, 1 год назад

помогите поставить глаголы в правильное время! There (be) many cases in which animals (take in) cubs that (not belong) to them, or even their species, like this adorable little pig. But I (never see)...

Математика, 7 лет назад

Помогите решить уравнение касательной к параболе...

Математика, 7 лет назад

Х^2-4х-32 Д=в^2-4ас= Х1= Х2=...

Математика, 8 лет назад

первое задание помагите пожалуйста буду благодарен...

Экономика, 8 лет назад

почему инфляцию в рыночной экономике не довести до нуля...