Математика, вопрос задал kk5683 , 2 года назад

Помогите пожалуйста найти самое большое натуральное значение параметра а, при котором неравенство не имеет решение

Приложения:

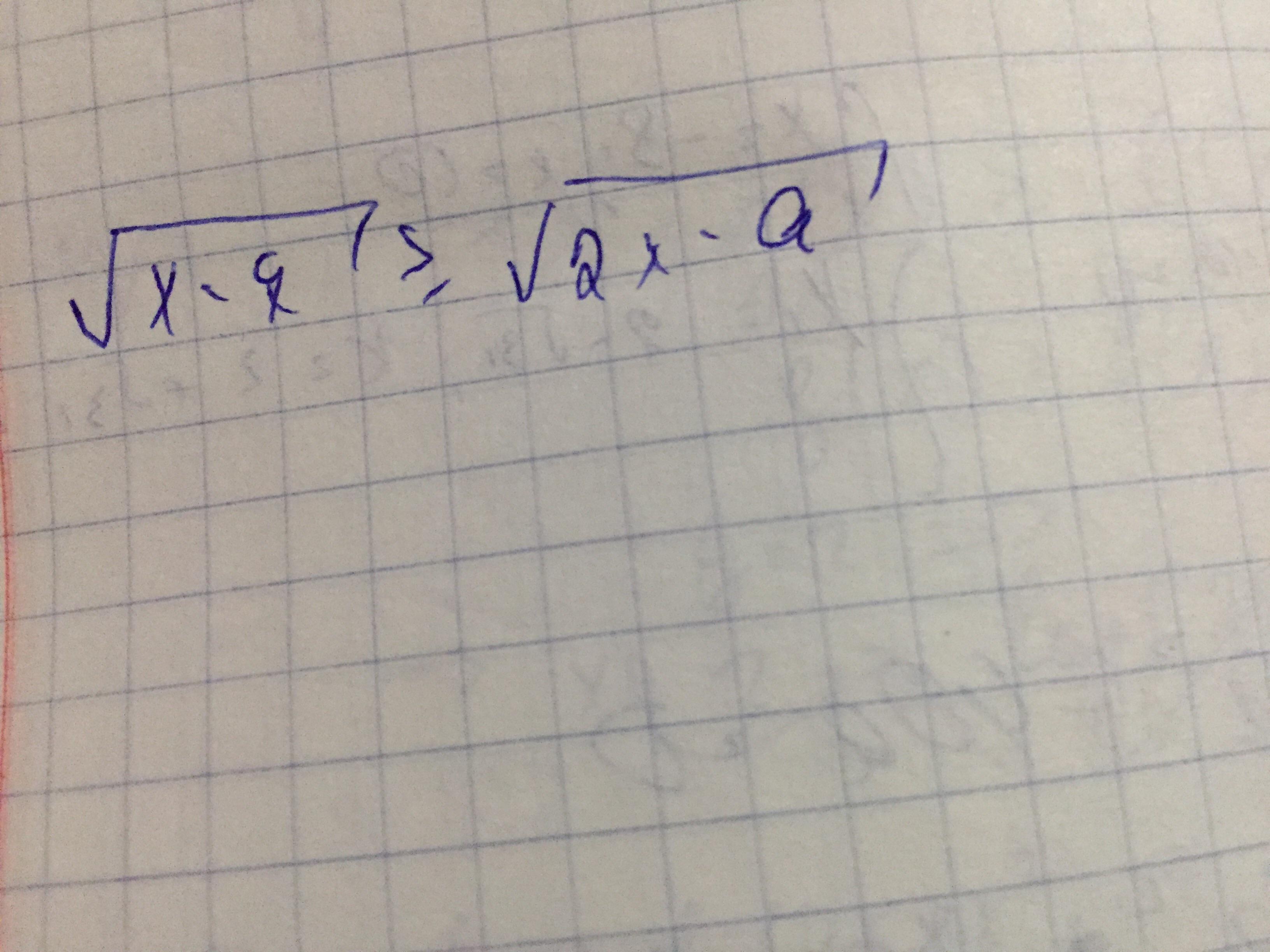
Ответы на вопрос

Ответил NNNLLL54

Ответ:

$\sqrt{x-7}\geq \sqrt{2x-a}\ \ \ \Leftrightarrow \ \ \ \left\{\begin{array}{l}x-7\geq 0\\2x-a\geq 0\\x-7\geq 2x-a\end{array}\right\ \ \left\{\begin{array}{l}x\geq 7\\x\geq \frac{a}{2}\\x\leq a-7\end{array}\right\\\\\\\left\{\begin{array}{l}x\geq \frac{a}{2}\\7\leq x\leq a-7\end{array}\right\ \ \left\{\begin{array}{l}x\geq \frac{a}{2}\\7\leq a-7\end{array}\right\ \ \left\{\begin{array}{l}x\geq 7\\a\geq 14\end{array}\right$

При a<14 неравенство не выполняется. Самое большое натуральное значение а, при котором неравенство не выполняется, - это 13 .

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Английский язык, 1 год назад

Помогите пожалуйста,срооочно надо)) составить предложения с can, could.

Русский язык, 1 год назад

Сочинение рассуждение на тему "Почему нужно писать грамотно"...

Литература, 2 года назад

СРОЧНО НАДО13. Определите, из какого произведения взят данный фрагмент. «На Кавказе тогда была война. По дорогам ни днём, ни ночью не было проезда. Чуть кто из русских отойдёт от крепости, татары или...

Алгебра, 2 года назад

сократите дробь (9х-3у)/(9х^2-у^2) если 3х-у не равно 0...

Химия, 7 лет назад

Вычислите массу и кол-во вещества натрия,необходимого для получения 30,5 г хлорида натрия с хлором...

География, 7 лет назад

В каких широтах расположены самая широкая и самая узкая часть материка южная Америка...