Математика, вопрос задал fyfarik , 7 лет назад

Помогите пожалуйста.
Математика. Автор: с.г.григорьев и задулина
Тема: Функция одной переменной
Предел функции

Приложения:

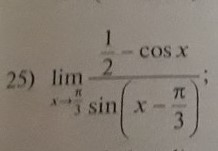
Ответы на вопрос

Ответил d3782741

0

Другой способ пока не приходит в голову:

$displaystylelim_{xtofrac{pi}{3}}dfrac{frac{1}{2}-cos x}{sinleft(x-frac{pi}{3}right)}=dfrac{0}{0}$

Значит можно применить правило Лопиталя

$displaystylelim_{xtofrac{pi}{3}}dfrac{frac{1}{2}-cos x}{sinleft(x-frac{pi}{3}right)}=displaystylelim_{xtofrac{pi}{3}}dfrac{left[frac{1}{2}-cos xright]'}{left[sinleft(x-frac{pi}{3}right)right]'}=displaystylelim_{xtofrac{pi}{3}}dfrac{sin x}{cosleft(x-frac{pi}{3}right)cdot 1}=medskip\=dfrac{sinfrac{pi}{3}}{cosleft(frac{pi}{3}-frac{pi}{3}right)}=dfrac{frac{sqrt{3}}{2}}{1}=dfrac{sqrt{3}}{2}$

Ответил fyfarik

0

Интересно,но такого правила мы ещё не знаем,ну или только я не знаю)))

Ответил d3782741

0

Ну, скорее всего значит там можно как-то преобразовать выражение под пределом. Котелок пока не доварил.

Ответил fyfarik

0

Лопиталя не походили, на 2 курсе то

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Русский язык, 1 год назад

Запишите числительные словами к 81/9+2/3 Из 11,1-2,2 Запишите числительные с существительными в указанных падежах Трое солдат (творительный,предложный) Пятеро бойцов (Винительный) Оч надо срочно...

Русский язык, 1 год назад

Прочитайте текст и выполните задания В1—В3 и С1. (1)Моржа Малышку доставили в зоопарк поздней осенью. (2)Ночью, когда подмораживает и лёд покрывает всю поверхность водоёма, она проделывает в...

Физика, 7 лет назад

Что общего и чем отличаются друг от друга наблюдение и эксперимент ?

Математика, 7 лет назад

Пожалуйста умоляюююююю дам 20 баллов...

Алгебра, 8 лет назад

1. Упростите выражение а) (х+1)²- (х-2)(х+4) б)(а+b)(a-b)(a²+b²) 2. Упростите выражение (5/2x-4y- 1/2y-x): 3/x-2y Помогите, пожалуйста! Срочно!

Биология, 8 лет назад

какие вещества необходимы человеку для правильного развития...