Помогите, пожалуйста !!!логарифмическое неравенство номер 1
Приложения:

Ответы на вопрос
Ответил belcatya
1
решение в приложении:
Приложения:
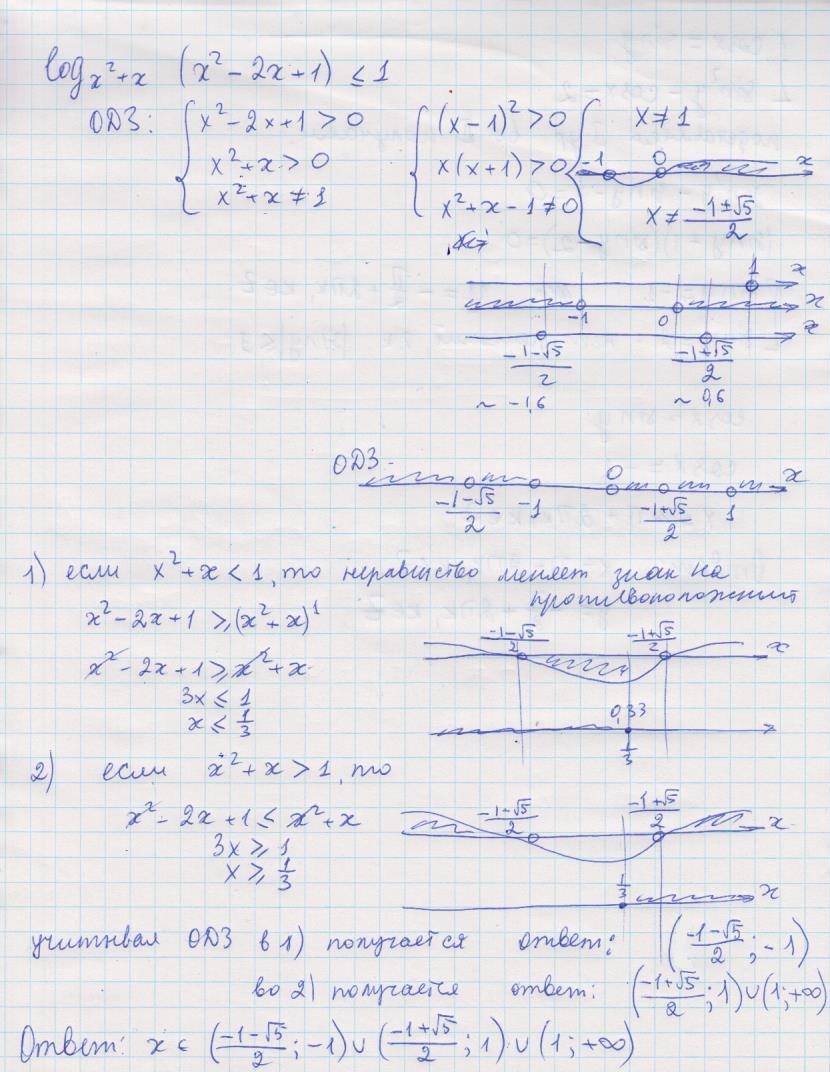
Ответил oganesbagoyan
1
Loq_(x² +x) (x² +2x +1) ≤ 1;
Loq_(x² +x) (x² +2x+1) ≤ Loq_(x² +x) (x² +x) ;
((x² +2x+1) -(x² +x)) ( (x² +x) -1) ≤ 0;
(x+1)(x² +x-1) ≤0;
(x+1) (x+(1+√5/)2)(x +(1 -√5)/2) ≤ 0;
(x+1/2 +1/2*√5)(x+1) (x +1/2 -1/2*√5) ≤ 0 ;
- + - +
------------------- ( -1/2 -1/2*√5 ) -------------- - 1 ------ (- 1/2 +1/2*√5) ---------
x∈( -∞ ; -1/2 -1/2*√5 ) U [ -1 ; - 1/2 +1/2*√5 ).
================ и л и =============================
совокупность двух систем неравенств
a) { 0<x² +x <1 ;x² +2x+1>x² +x ;
b) { x² +x > 1 ; x² +2x+1 < x² +x ;
арифметику нужно проверить
Loq_(x² +x) (x² +2x+1) ≤ Loq_(x² +x) (x² +x) ;
((x² +2x+1) -(x² +x)) ( (x² +x) -1) ≤ 0;
(x+1)(x² +x-1) ≤0;
(x+1) (x+(1+√5/)2)(x +(1 -√5)/2) ≤ 0;
(x+1/2 +1/2*√5)(x+1) (x +1/2 -1/2*√5) ≤ 0 ;
- + - +
------------------- ( -1/2 -1/2*√5 ) -------------- - 1 ------ (- 1/2 +1/2*√5) ---------
x∈( -∞ ; -1/2 -1/2*√5 ) U [ -1 ; - 1/2 +1/2*√5 ).
================ и л и =============================
совокупность двух систем неравенств
a) { 0<x² +x <1 ;x² +2x+1>x² +x ;
b) { x² +x > 1 ; x² +2x+1 < x² +x ;
арифметику нужно проверить
Новые вопросы