Помогите пожалуйста, как можно быстрее (задания написаны на украинском языке)
Приложения:

Ответы на вопрос
Ответил Miroslava227
0
Ответ:
1.
1)
- общий вид
В точке А:
2)
- общий вид
В точке В:
3)
- общий вид
В точке С:
4)
- общий вид
В точке D:
2.
При S(3; 42):
Ответ:
3.
1)
2)
3)
4)
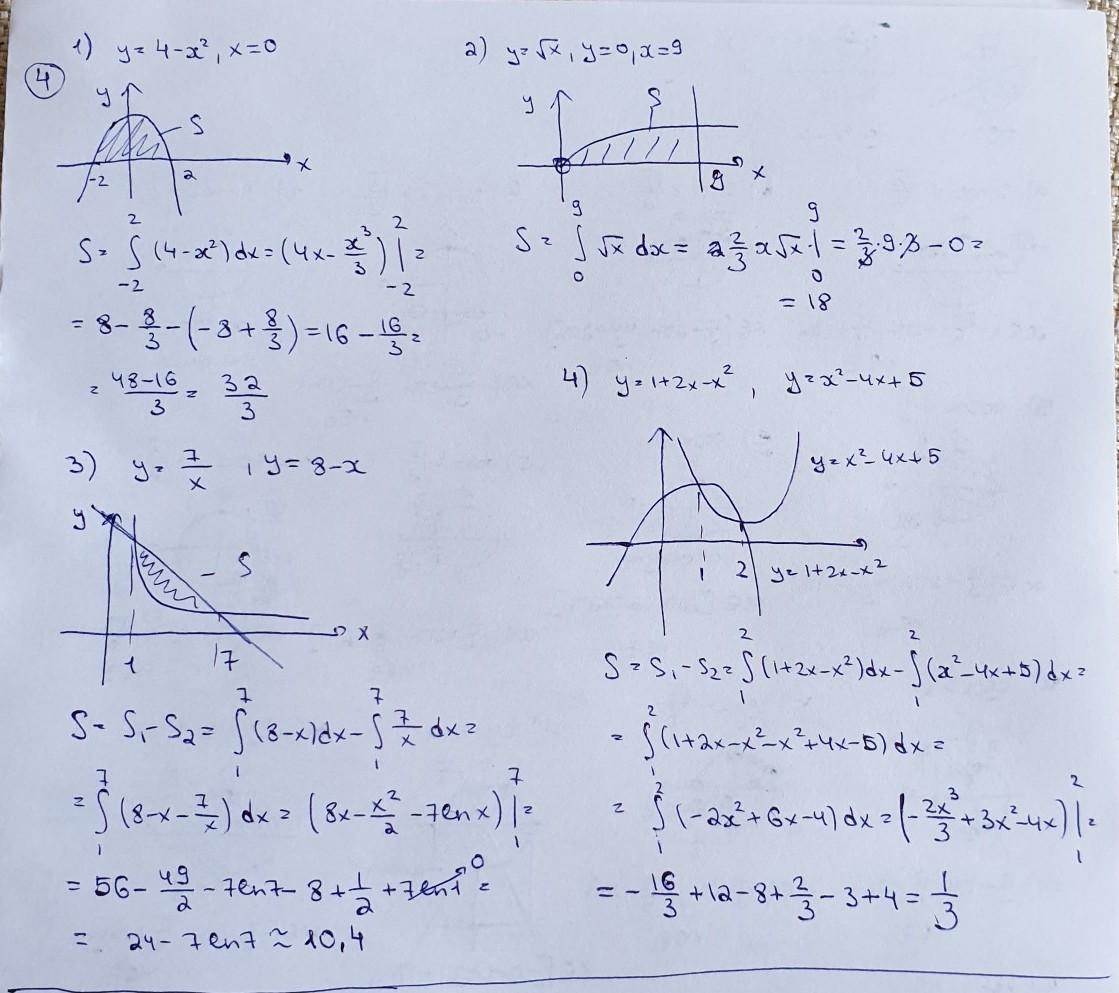
4.
На фото
5.
на фото
Приложения:
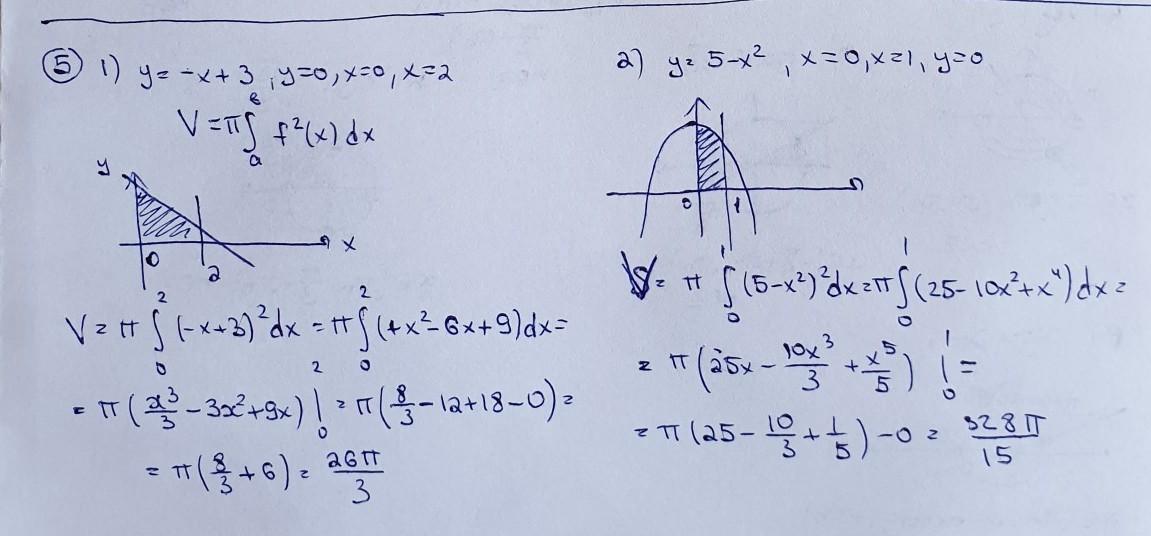
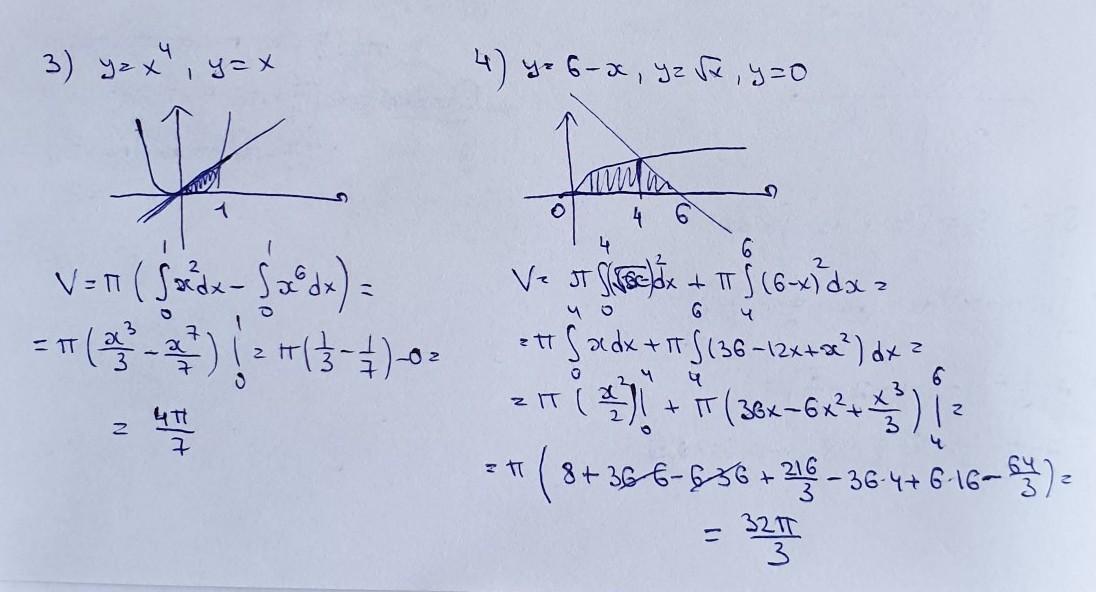
Новые вопросы
Русский язык,
1 год назад
Русский язык,
1 год назад
Математика,
2 года назад
Английский язык,
2 года назад
Физика,
8 лет назад