Математика, вопрос задал HOLTZMANN1 , 2 года назад

ПОМОГИТЕ, ПОЖАЛУЙСТА, ИССЛЕДУЙТЕ НА СХОДИМОСТЬ УКАЗАННЫЙ РЯД

Приложения:

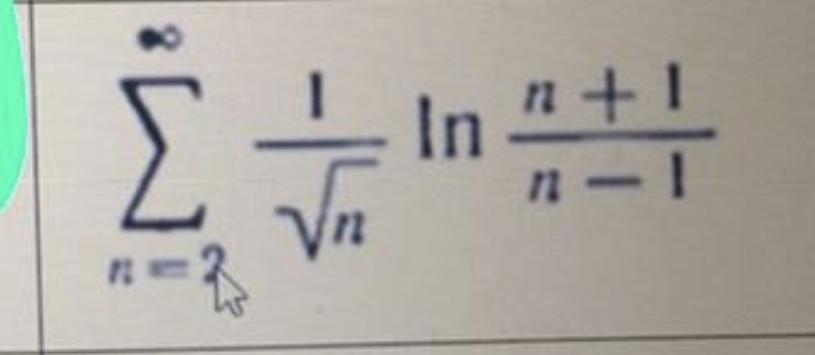
Ответы на вопрос

Ответил pushpull

Ответ:

Пошаговое объяснение:

давайте сразу начнем упрощать общий член

$\displaystyle \lim_{n \to \infty} ln\bigg (\frac{n+1}{n-1} \bigg ) = \lim_{n \to \infty} \bigg (-1+\frac{n+1}{n-1}\bigg )= \lim_{n \to \infty} \frac{2}{n-1}$

$\displaystyle \lim_{n \to \infty}(n-1) = \lim_{n \to \infty} n$

учитывая эти свойства, мы получим такой предел

$\displaystyle \lim_{n \to \infty}\frac{2}{\sqrt{n} (n-1)} = \lim_{n \to \infty} \frac{2}{n^{3/2}}$

исследуем сходимость ряда при помрщи интегрального признака Коши

$\displaystyle \int\limits^{\infty}_2 {\frac{2}{n^{3/2}} } \, dn=\bigg (-\frac{2}{\sqrt{n} }\bigg )\bigg |_2^\infty= \lim_{n \to \infty}\biff (-\frac{2}{\sqrt{n} } \bigg )+\sqrt{2} =0+\sqrt{2} =\sqrt{2}$

несобственный интеграл сходится, значит сходится и наш ряд

HOLTZMANN1: а как ln стал -1?

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Русский язык, 1 год назад

как выделять корни в словах клюв, плод, гараж, ландыш, рассказ, след, пруд, гриб, шкаф, этаж, арбуз, солдат, поэт...

Русский язык, 1 год назад

почему человеку интересно наблюдать за явлениями природы?сочинение пожалуйста помогите...

Українська література, 2 года назад

Чому Петро Шраменко довгий час не міг одружитися із Лесею?

Биология, 2 года назад

4. Цветок, у которого есть чашечка и венчик. 1) правильный цветок 2) цветок с двойным околоцветником 3) неправильный цветок 4) цветок с простым околоцветником...

Биология, 8 лет назад

1. На русский язык переводится словом "растения": А. "ботанэ"; Б. "биос"; В. "дендро"; Г. "логос". 2. Из перечисленных растений выберите двулетнее растение: А. рожь; Б. редис;...

Математика, 8 лет назад

Книга на 25 % дороже альбома.На сколько процентов альбом дешевле книги?