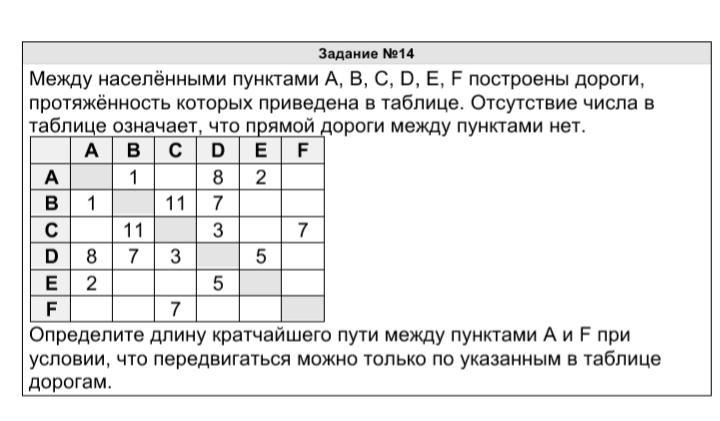
Помогите пожалуйста. Информатика, тема графы

Для решения этой задачи можно воспользоваться Алгоритмом Дейкстры.

Суть алгоритма следующая:

1. Выбираем начальную вершину, её метка 0.

2. Если все вершины просмотрены - конец.

Иначе, из непросмотренных ранее вершин выбирается вершина с минимальной меткой - u.

3. Рассматриваем все вершины, инцидентные (связанные ребром с) рассматриваемой и не просмотренные ранее - "соседи". Для каждой такой вершины v рассмотрим новую длину пути, равную сумме метки рассматриваемой вершины u и длины ребра uv, соединяющего рассматриваемую вершину u с "соседом" v.

4. Если полученная новая длина меньше значения метки вершины-"соседа" v, метка вершины v заменяется на полученным значением.

5. Рассмотрев всех "соседей" выбранной вершины, помечаем её просмотренной и переходим в пункт 2.

В конце концов у каждой вершины, связной с начальной (возможно через промежуточные вершины) будет метка, обозначающая длину кратчайшего пути к ней от начальной.

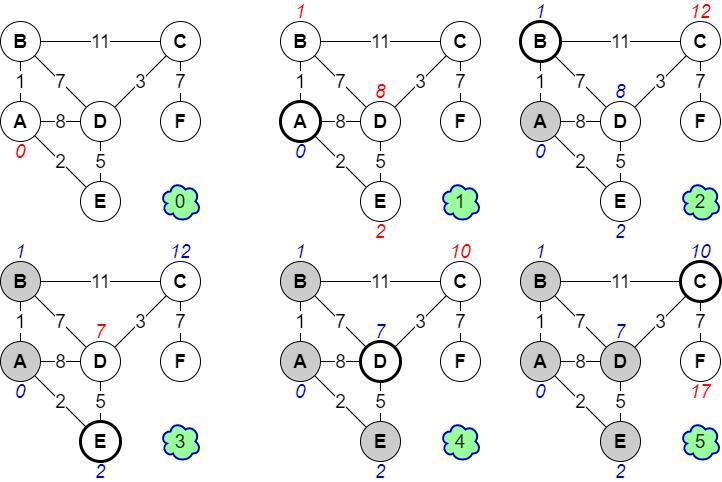
В качестве решения к решению прикреплено приложение, ниже распишу обозначения:

• "Облачко" с цифрой - номер шага.
• Красный текст - метка поставленная на текущем шаге.
• Синий текст - метка, поставленная ранее.
• Вершина закрашена - вершина просмотрена.
• Вершина имеет толстую границу - вершина рассматривается на текущем шаге.

Перейдём к нашей задаче.

Шаг 0. Построили граф по заданной матрице. Начальной вершине A присвоили метку 0.

Шаг 1. Рассматриваем вершину А. Её "соседи" - вершины B, D и E. Их метки равны весу соответствующих рёбер - AB (1), AD (8) и AE (2). Вершину А помечаем просмотренной.

Шаг 2. Рассматриваем вершину B, так как её метка минимальна (2). Её "соседи" из непросмотренных - вершины С и D. Метка вершины C равна весу ребра BC + метка вершины B, то есть 11 + 1 = 12. Вершина D уже имеет метку 8, новая длина же получится 7 + 1 = 8, то есть тут никаких изменений. Вершину B помечаем просмотренной.

Шаг 3. Рассматриваем вершину E (метка 2). Её непросмотренный "сосед" - вершина D, она претендует на метку 5 + 2 = 7, что меньше уже имеющейся у неё метки 8. Тогда новая метка D - 8. Вершину E помечаем просмотренной.

Далее рассматривать будем менее подробно.

Шаг 4. Вершина D инцидента вершине C, новая метка 7 + 3 = 10 меньше предыдущей (12) значит ставим новую метку.

Шаг 5. Рассматриваем вершину С. Из подходящих соседей только вершина F, она получает метку 10 + 7 = 17.

Вершину F нет смысла рассматривать, так как она не связана ни с одной непросмотренной вершиной.

Так как вершина F имеет метку 17, то длина кратчайшего пути от начальной вершины A к вершине F равна 17.

Ответ: 17.