Алгебра, вопрос задал Maria2838 , 7 лет назад

помогите пожалуйста

если нужен рисунок то с ним

я уже в третий раз выкладываю удаляется в чем может быть проблема?

Приложения:

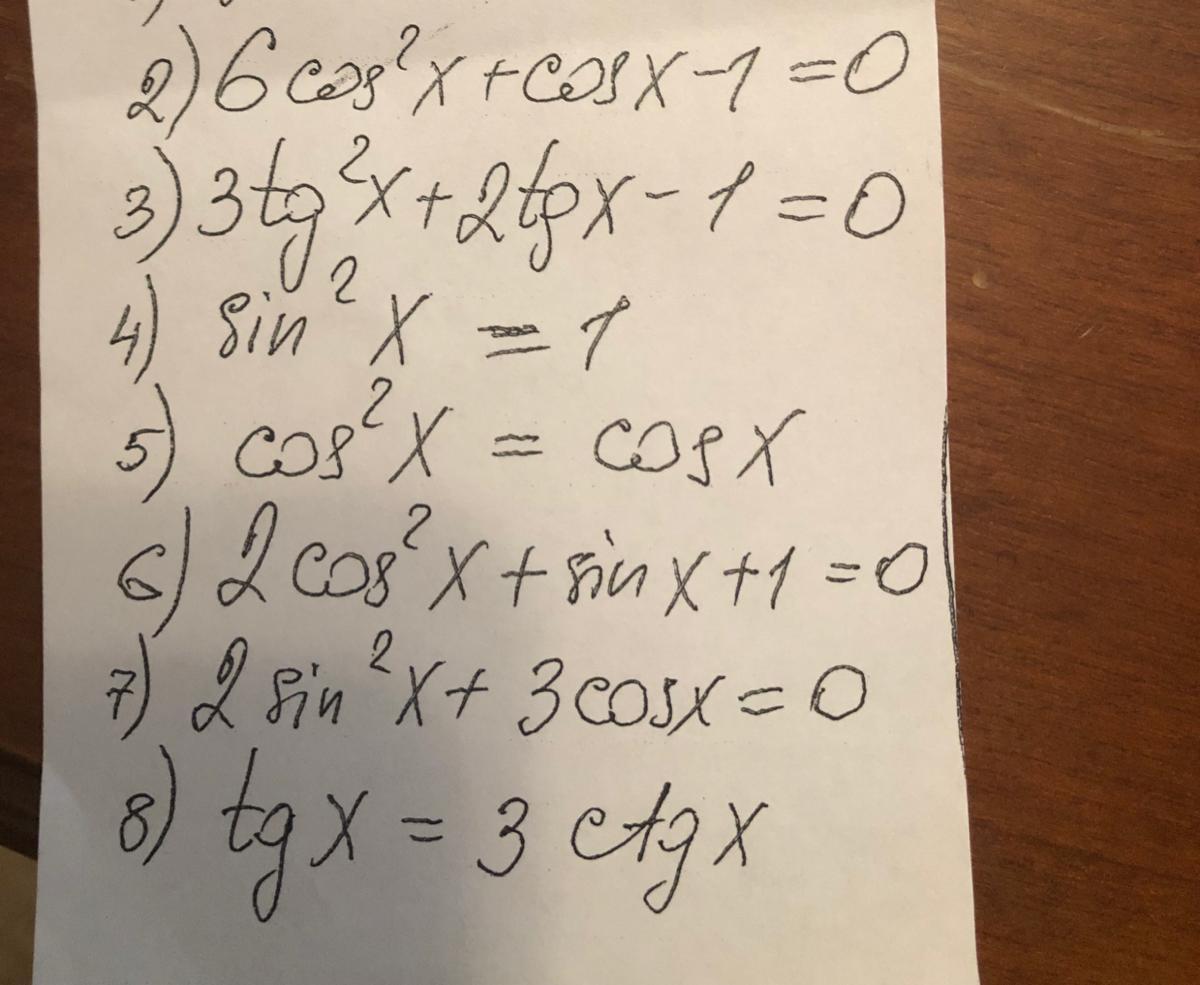
Ответы на вопрос

Ответил sunnatxoja7

$6cos^2x+cosx-1=0\D=1+4*6=25=5^2\cosx_1=frac{-1-5}{12}=-frac{1}{2}\\cosx_2=frac{-1+5}{12}=frac{1}{3}\\ x_1=pm(pi-frac{pi }{3})+2pi k, k in Z=pmfrac{2pi }{3}+2pi k, k in Z\x_2=pm arccos(frac{1}{3} )+2pi k ,k in Z$

$3tg^2x+2tgx-1=0\D=4+4*3=16=4^2\tgx_1=frac{-2-4}{6}=-1\ tgx_2=frac{-2+4}{6}=frac{1}{3}\\left { {{x_1=-frac{pi }{4}+pi k, k in Z} atop {x_2=arctg(frac{1}{3})+pi k, k in Z )}} right.$

$sin^2x=1\sinx=pm1\\left { {{x_1=frac{pi }{2}+2pi k,k in Z } atop {x_2=-frac{pi }{2}+2pi k,k in Z}} right.$

$cos^2x=cosx\cos^2x-cosx=0\cosx(cosx-1)=0\\left { {{cosx=0} atop {cosx=1}} right. =>left { {{x_1=frac{pi }{2}+pi k,k in Z} atop {x_2=2pi k, k in Z}} right.$

$2cos^2x+sinx+1=0\2(1-sin^2x)+sinx+1=0\2-2sin^2x+sinx+1=0\2sin^2x-sinx-3=0\D=1+24=25=5^2\sinx_1=frac{1-5}{4}=-1\sinx_2=frac{1+5}{4}=frac{3}{2}=>x in emptyset\\x_1=-frac{pi }{2}+2pi k,k in Z$

$2sin^2x+3cosx=0\2(1-cos^2x)+3cosx=0\2-2cos^2x+3cosx=0\2cos^2x-3cosx-2=0\D=9+16=25=5^2\cosx_1=frac{3-5}{4}=-frac{1}{2}\cosx_2=frac{3+5}{4}=2 =>x in emptyset\ \x_1=pm(pi-frac{pi }{3})+2pi k, k in Z=pmfrac{2pi }{3}+2pi k, k in Z$