Математика, вопрос задал veligasymov1977 , 2 года назад

помогите пожалуйста даю 15 балов!!!!​

Приложения:

Ответы на вопрос

Ответил Alnadya
0

Решение.

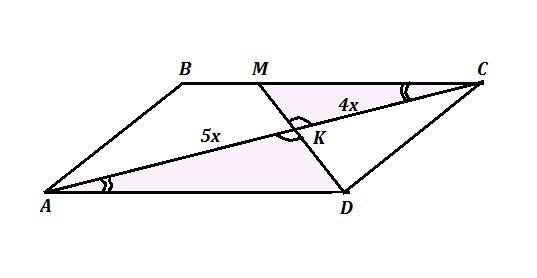
ABCD - параллелограмм , АС - диагональ , АК:КС=5:4 , DK ∩ BC = M

Найти:  ВМ:МС .

ΔAKD ~ ΔМКС  по двум углам ( ∠МСА=∠СAD как внутренние накрест лежащие при BC || AD и секущей АС , ∠МКС=∠AKD  как вертикальные)

\bf \dfrac{MC}{AD}=\dfrac{MK}{KD}=\dfrac{CK}{KA}\ \ \Rightarrow \ \ \ \dfrac{MC}{AD}=\dfrac{4}{5}  

Но  AD=BC как противоположные стороны параллелограмма, поэтому

\bf \dfrac{MC}{AD}=\dfrac{MC}{BC}=\dfrac{4}{5}\ \ \ \Rightarrow \ \ \ MC=4x\ ,\ BC=5x\\\\\\BC=BM+MC\ \ ,\ \ 5x=BM+4x\ \ ,\ \ \ BM=5x-4x=x\ \ \ \Rightarrow \\\\\\\dfrac{BM}{MC}=\dfrac{x}{4x}=\dfrac{1}{4}  

Ответ:  Е) .

Приложения:
Предыдущий вопрос
Следующий вопрос
Новые вопросы
Русский язык, 1 год назад
В каком предложении выделенное слово является прилагательным? 1. Беседа протекала МИРНО. 2. Мы жили очень СПОКОЙНО. 3. Старик ЛЕГКО встал и, не прощаясь, ушел 4. Помещение не убиралось давно и...
Русский язык, 1 год назад
Напишите пожалуйста небольшой отзыв об стихотворении М.Ю.Лермонтова "Ангел" Обьём должен быть не меньше пол странички тетради НЕ КОПИРАЙТИТЬ ПОЛНОСТЬЮ С ДРУГИХ САЙТОВ, ЭТО Я И САМ МОГУ. МОЖЕТЕ БРАТЬ...
Алгебра, 2 года назад
1.дріб менший за 0,5? а) 13/27. б) 3/4. г) 34/51. 2.скоротній дріб а) 13/27. б) 3/4. г) 34/51​...
Физика, 2 года назад
На наклонной плоскости с углом наклона 450 к горизонту стоит цилиндр с радиусом основания 3 см. При какой наибольшей высоте цилиндр не опрокинется?
Биология, 7 лет назад
Вы, вероятно, не раз бывали на озере или речке. Какие организмы, живущие в пресных водоёмах, вы знаете?
Литература, 7 лет назад
Каким словом можно заменить слово щедро 10 б.