Помогите пожалуйста дам 100 баллов

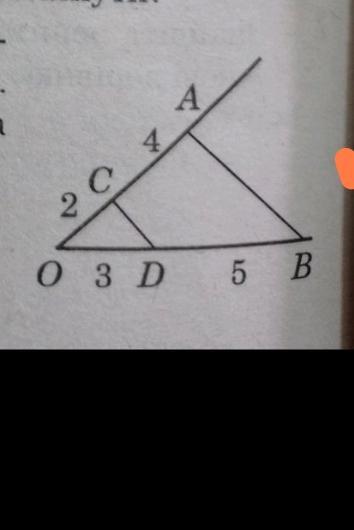
На сторонах ОA ОВ кута О відкладено вiдрiзки ОС = 2 см; СА = 4 см; OD = 3 см; DB = 5 см. Знайдіть відношення площі чотирикутника ABDC до площі трикутника ОАВ.

Ответ:

Отношение площади четырехугольника ABDC к площади треугольника ОАВ равно 7/8.

Объяснение:

На сторонах ОА и ОВ угла А отложены отрезки ОС = 2 см; СА = 4 см, OD = 3 см; DB = 5 см. Найдите отношение площади четырехугольника ABDC к площади треугольника ОАВ.

Дано: ∠О;

ОС = 2 см; СА = 4 см, OD = 3 см; DB = 5 см.

Найти: S(ABDС) : S(ОAB)

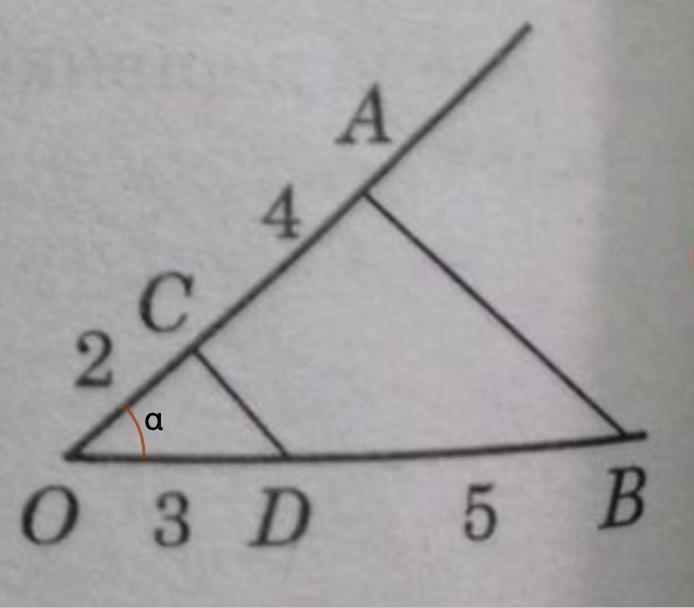
Решение:

• Площадь треугольника равна половине произведения сторон на синус угла между ними.

Пусть ∠О = α.

  (см²)

  (см²)

 (см²)

Теперь можем найти отношение S(ABDС) : S(ОAB).

Отношение площади четырехугольника ABDC к площади треугольника ОАВ равно 7/8.

#SPJ1