Помогите пожалуйста, буду очень благодарен
Ответы на вопрос
Ответ:
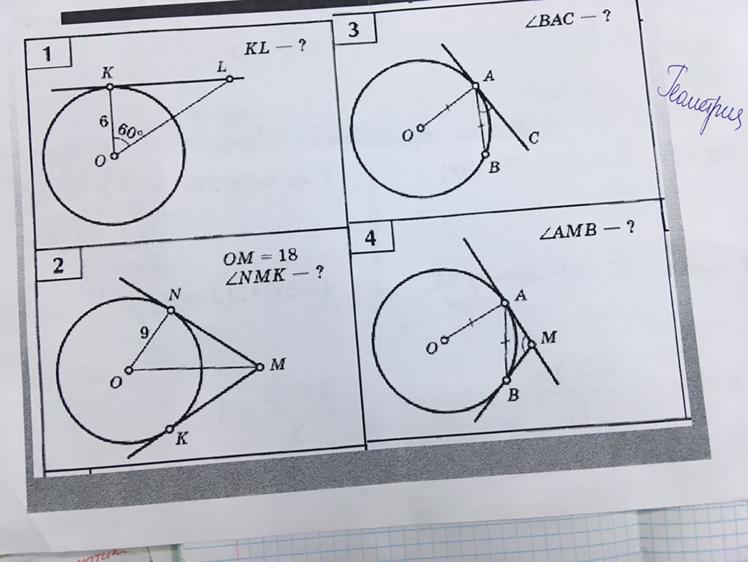
Пошаговое объяснение: №1 ΔКОL-прямоугольный, т.к. радиус ОК⊥КL (касательная перпендикулярна радиусу, проведённому в точку касания), ⇒КL= OK·tg60° = 6·√3 №2. Δ ОMN -прямоугольный, т.к. радиус ОN⊥MN (касательная перпендикулярна радиусу, проведённому в точку касания), по условию ON=1/2 ·OM (9=1/2 ·18) ⇒∠NMO=30° (по св-ву катета, лежащего против угла в 30°), ⇒∠NMK =30°·2=60° (по св-ву касательных, проведённых из одной точки к окружности). №3. ΔОАВ -равносторонний, т.к. ОА=ОВ=R(радиусы окружности), а ОА =АВ по условию, ⇒ОА=ОВ=АВ, ⇒все углы треугольника равны по 60°, ⇒∠ОАВ=60°. ∠ОАС=90° (касательная перпендикулярна радиусу)⇒∠ВАС=90°-60°°=30°. №4 ΔОАВ -равносторонний, т.к. ОА=ОВ=R(радиусы окружности), а ОА =АВ по условию, ⇒ОА=ОВ=АВ, ⇒все углы треугольника равны по 60°, ⇒∠ОАВ=60°. ∠ОАС=90° (касательная перпендикулярна радиусу)⇒∠ВАМ=90°-60°°=30°. Но ΔАМВ равнобедренный (по св-ву касательных, проведённых из одной точки М)⇒∠АВМ=∠∠ВАМ=30°, тогда ∠АМВ= 180° -(30°+30°)= 120°.