Помогите пожалуйста!!! Буду благодарна.
1. Найдите длину стороны BC прямоугольника ABCD, если AB=7, а его площадь равна 56.
2. В треугольнике ABC AB=4, BC=6, AC=9. Найдите длину средней линии MN, если известно, что она параллельна BC.
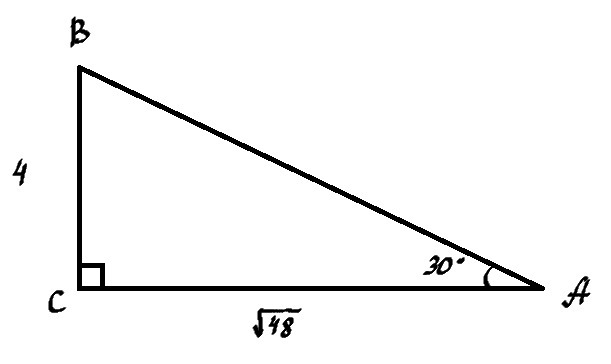
3. В прямоугольном треугольнике ABC угол С прямой. Найдите периметр данного треугольника, если угол A=30 градусов, AC= корень из 48, а BC= 4.

1. Площадь прямоугольника находится по формуле S=ab , где a, b - длина и ширина прямоугольника.
Дано: S=56, a=7
Найти: b



Ответ: ВС = 8.

2. Длина средней линии в треугольнике равна половине длины стороны, которой она параллельна.

МN║BC
ВС = 6



Ответ: MN = 3.

3. В прямоугольном треугольнике напротив угла в 30° лежит катет в два раза меньше гипотенузы.

АВ = 2ВС

АВ = 2*4 = 8.
Периметр - это сумма длин всех сторон.


Ответ: