Математика, вопрос задал asdagfrra , 2 года назад

Помогите пожалуйста. Буду благодарен

Приложения:

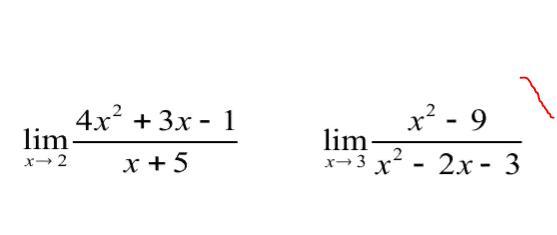
Ответы на вопрос

Ответил pushpull

Ответ:

Пошаговое объяснение:

1) с первым пределом проблем нет. тут никаких неопределенностей нет

$\lim_{x \to 2} \frac{4x^2+3x-1}{x+5} = \frac{4*2^2+3*2 -1}{2+5} =3$

2) со вторым похуже. тут двустороннего предела нет

будем рассматривать предел справа и слева

слева

$\lim_{x \to {3^-} }\frac{x^2-9}{x^2-2x-3}$ запишем в виде

$\lim_{x \to {3^-} }(x^2-9) * \lim_{x \to {3^-} }} \frac{1}{x^2-2x-3}$

$\lim_{x \to {3^-} }(x^2-9) = 27$

поскольку $\lim_{x \to {3^-}} (x^2-2x-3) =0$ и (x^2-2x-3) < 0 для х < 3, то

$\lim_{x \to {3^-}} \frac{1}{x^2-2x-3 } = -\infty$

и получим

$\lim_{x \to {3^-} }\frac{x^2-9}{x^2-2x-3}= 27*(-\infty) =- \infty$

справа

для этого предела все рассуждения те же, за исключением того, что

(x^2-2x-3) > 0 для х > 3, поэтому $\lim_{x \to {3^+}} \frac{1}{x^2-2x-3 } = +\infty$

и тогда

$\lim_{x \to {3^+} }\frac{x^2-9}{x^2-2x-3}= 27*(+\infty) =+\infty$

Новые вопросы

Русский язык, 1 год назад

Английский язык, 1 год назад

Математика, 2 года назад

Химия, 2 года назад

Математика, 7 лет назад

История, 7 лет назад