Алгебра, вопрос задал balichmaks , 6 лет назад

Помогите пожалуйста. Алгебра все на скриншоте

Приложения:

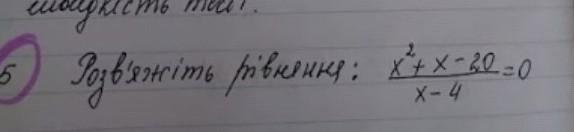
Ответы на вопрос

Ответил Vopoxov

Ответ:

-5

Объяснение:

Для решения всего уравнения нужно найти значения х, когда числитель равен нулю, при этом исключить такие значения, при которых знаменатель выражения образается в ноль:

$\small\frac{{x}^{2} + x - 20}{x - 4} = 0 \: \: \: {< }{= > } \left \{ \begin{array}{l} { {x}^{2} + x - 20} = 0 \\ {x - 4} \neq 0\end{array} \right. \: { < = > }...\\ \: no \: meop. \: Buema: \: \\ {x}^{2} + x - 20 = (x - 4)(x + 5) \\ \\ ...{ < = > } \left \{ \begin{array}{l} { ( {x} - 4)(x + 5)} = 0 \\ {x - 4} \neq 0\end{array} \right. { < = > }\left \{ \begin{array}{l} \left[ \begin{array}{l} { x + 5} = 0 \\ {x - 4} = 0\end{array} \right. \\ {x - 4} \neq 0\end{array} \right. \\ \left \{ \begin{array}{l} \left[ \begin{array}{l} { x } = - 5\\ {x = 4} \end{array} \right. \\ {x } \neq 4\end{array} \right. < = > \: \: \: x = - 5$