Математика, вопрос задал mardasovayna , 2 месяца назад

помогите пожалуйста 9

Приложения:

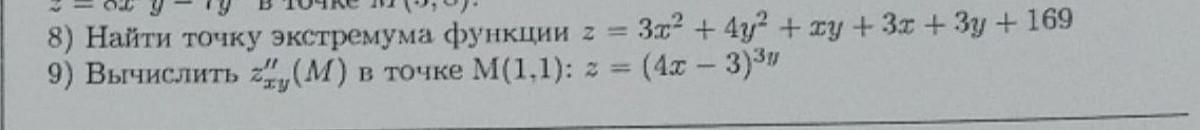
Ответы на вопрос

Ответил shadowmarder20

1

Відповідь:

12

Покрокове пояснення:

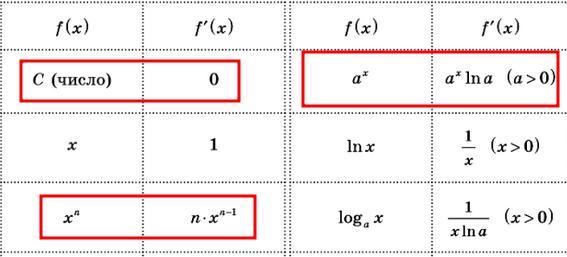
Щоб знайти $z''_{xy}$ . Нам потрібно спочатку знайти $z'_{x}$ , це буде складена похідна ми маємо помножити похідну зовнішньої функції (степеня) на похідну внутрішньої (те, що в дужках), ось так:

$z'_{x}=((4x-3)^{3y})'=((4x-3)^{3y})'*(4x-3)'=3y(4x-3)^{3y-1} *(4x)'-(3)'=3y(4x-3)^{3y-1} *4-0=12y(4x-3)^{3y-1}$

Тепер шукаємо $z''_{xy}$ :

$z''_{xy}=(12y(4x-3)^{3y-1})'= (12y)'(4x-3)^{3y-1}+12y((4x-3)^{3y-1})'=12(4x-3)^{3y-1}+12y((4x-3)^{3y-1})'$

$((4x-3)^{3y-1})'$ це складена похідна, ми маємо взяти похідну зовнішньої функції (показникової, $a^{y}$ , тільки замість a - $(4x-3)$ , а замість y - $(3y-1)$ ) і помножити її на похідну внутрішньої (3y-1):

$((4x-3)^{3y-1})'=((4x-3)^{3y-1})'* (3y-1)'=((4x-3)^{3y-1})'*3=ln(4x-3)*(4x-3)^{3y-1}*3$ Повертаємося до попереднього виразу:

$z''_{xy}=12(4x-3)^{3y-1}+12y((4x-3)^{3y-1})'=12(4x-3)^{3y-1}+12y*ln(4x-3)*(4x-3)^{3y-1}*3=12(4x-3)^{3y-1}+36y*ln(4x-3)*(4x-3)^{3y-1}$

$z''_{xy}(M(1,1))=12(4*1-3)^{3*1-1} +36*1*ln(4*1-3)*(4*1-3)^{3*1-1}=12*1^2+36ln(1)*1^2=12+36*0*1=12$

Приложения:

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Математика, 2 месяца назад

Всё расписать, срочно. Вычислить несобственный интеграл или доказать его несовпадение:(на фото)...

Математика, 2 месяца назад

решите быстро быстро!!!!

Алгебра, 2 месяца назад

Дуже потрібна допомога, терміново!

Математика, 2 месяца назад

К набору 3; 4; 5 добавьте еще одно число так, чтобы его наибольшее значение не изменилось и опишите словами местонахождение новой точки...

География, 6 лет назад

Чем объяснить различия в расположении полезных ископаемых магматического и осадочного происхождения...

Английский язык, 6 лет назад

Choose the correct answer. 1 I haven't made anything / any good for dinner yet. 2 Emily Johnson isn't at our school any longer/ any good. She moved last term. 3 This film isn't any more / any...