Помогите пожалуйста, 7 класс, выполните с доказательством и рисунками
Приложения:

Ответы на вопрос
Ответил JoridaP
1
Ответ:
В равнобедренном треугольнике медианы, проведенные к боковым сторонам, равны.
Доказательство: Пусть ABC - равнобедренный треугольник (AC = BC), AK и BL - его медианы. Тогда треугольники AKB и ALB равны по второму признаку равенства треугольников. У них сторона AB общая, стороны AL и BK равны как половины боковых сторон равнобедренного треугольника, а углы LAB и KBA равны как углы при основании равнобедренного треугольника. Так как треугольники равны, их стороны AK и LB равны. Но AK и LB - медианы равнобедренного треугольника, проведённые к его боковым сторонам.
Приложения:
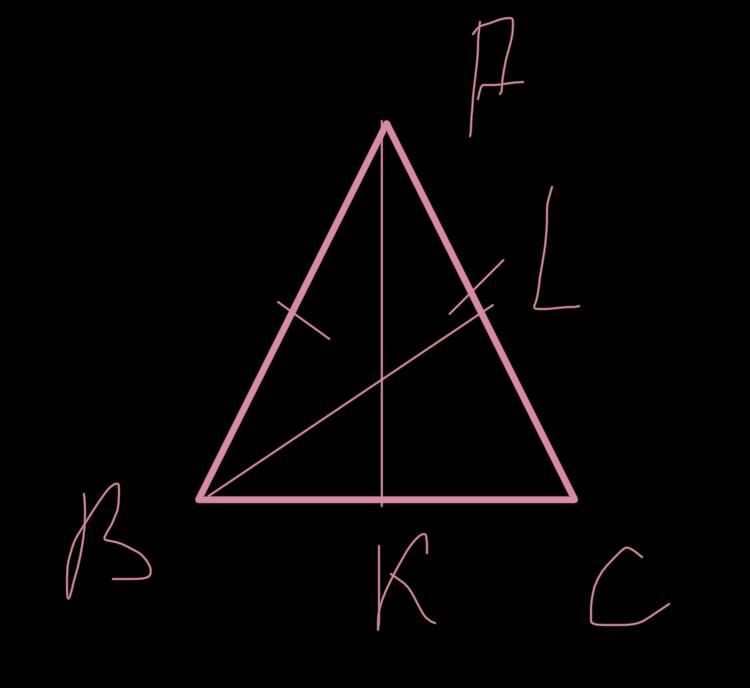
Новые вопросы
Русский язык,
1 год назад
Русский язык,
1 год назад
Алгебра,
6 лет назад
Физика,
6 лет назад
Математика,
8 лет назад