Математика, вопрос задал mardasovayna , 2 месяца назад

помогите пожалуйста ​

Приложения:

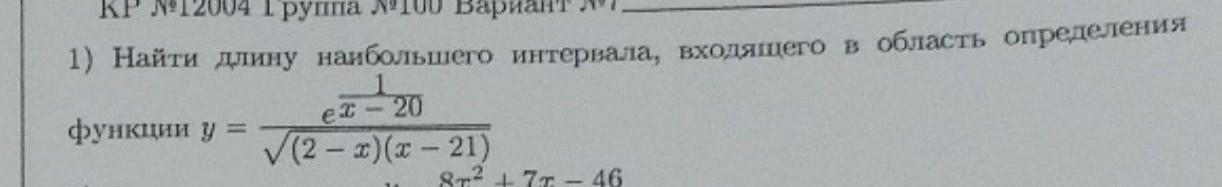
Ответы на вопрос

Ответил Alnadya
1

Решение .

Найдём область определения функции .

\bf y=\dfrac{\dfrac{1}{e^{x}-20}}{\sqrt{(2-x)(x-1)}}\ \ \Rightarrow \ \ \ \left\{\begin{array}{l}\bf e^{x}-20\ne 0\\\bf (2-x)(x-21) > 0\end{array}\right \\\\\\\left\{\begin{array}{l}\bf e^{x}\ne 20\\\bf (x-2)(x-21) < 0\end{array}\right \ \ \left\{\begin{array}{l}\bf x\ne ln20\\\bf x\in (\ 2\ ;\ 21\ )\end{array}\right\ \ \ \Rightarrow \\\\\\x\in (\ 2\ ;\ ln20\ )\cup (\ ln20\ ;\ 21\ )          

Найдём длину d наибольшего интервала, входящего в ООФ .

\bf 2=lne^2\approx ln\, 7,389\ \ ,\ \ \ ln20\approx 2,9957\ \ ,\ \ \ 21=lne^{21}\approx ln\, 1318815734,48  

\bf d=lne^{21}-ln20=ln\dfrac{e^{21}}{20}\approx 65940786,7                

Предыдущий вопрос
Следующий вопрос
Новые вопросы