Алгебра, вопрос задал rubkub31 , 1 год назад

помогите пожалуйста

Приложения:

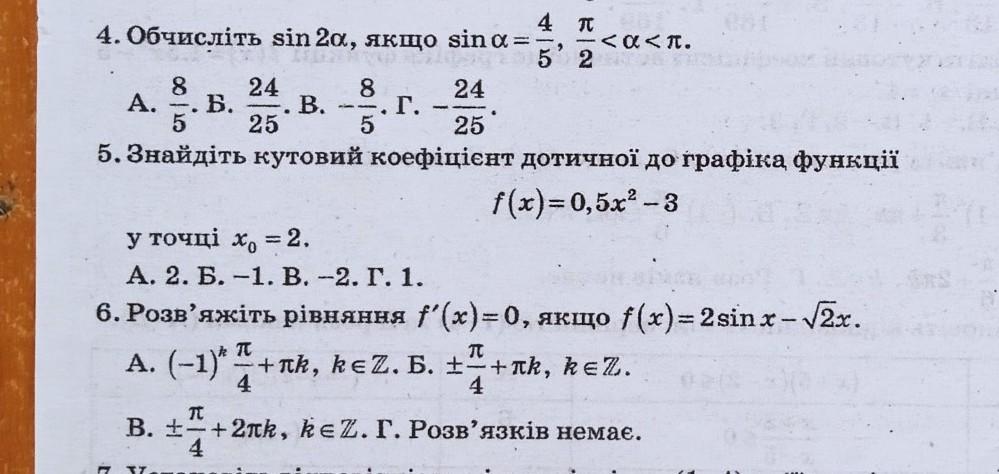
Ответы на вопрос

Ответил axatar

Ответ и Объяснение:

4. Требуется вычислить sin2α, если $\tt sin\alpha =\dfrac{4}{5}, \; \dfrac{\pi }{2} < \alpha < \pi .$

Во второй четверти, то есть если $\tt \dfrac{\pi }{2} < \alpha < \pi$ , cosα < 0. Тогда из основного тригонометрического тождества

sin²α+cos²α = 1

получим, что при $\tt \dfrac{\pi }{2} < \alpha < \pi$

$\tt cos\alpha =-\sqrt{1-sin^2\alpha }.$

Подставим известное значение $\tt sin\alpha =\dfrac{4}{5}:$

$\tt cos\alpha =-\sqrt{1-\bigg (\dfrac{4}{5} \bigg )^2 }=-\sqrt{1-\dfrac{16}{25} }=-\sqrt{\dfrac{9}{25} }=-\dfrac{3}{5} .$

Теперь остаётся применить тождество sin2α = 2·sinα·cosα:

$\tt sin2\alpha =2 \cdot \dfrac{4}{5} \cdot (-\dfrac{3}{5} )=-\dfrac{24}{25} .$

Ответ: Г) $\tt -\dfrac{24}{25}$ .

5. Требуется найти угловой коэффициент касательной к графику функции

f(x) = 0,5·x²-3

в точке x₀ = 2.

Известно, что угловой коэффициент касательной к графику функции y = f(x), проведённой в точке x₀, равен значению производной в точке x₀, то есть k = f'(x₀).

Известны табличные производные: (xⁿ)' = n·xⁿ⁻¹, (const)' = 0.

Найдём производную от функции:

f'(x) = (0,5·x²-3)' = 0,5·(x²)'-(3)' = 0,5·2·x-0 = x.

Тогда

k = f'(2) = 2.

Ответ: А) 2.

6. Требуется решить уравнение f'(x) = 0, если f(x) = 2·sinx - $\sqrt{2}$ ·x.