Помогите пожалуйста!
Приложения:
Ответы на вопрос
Ответил bertramjeratire
1
Ответ:
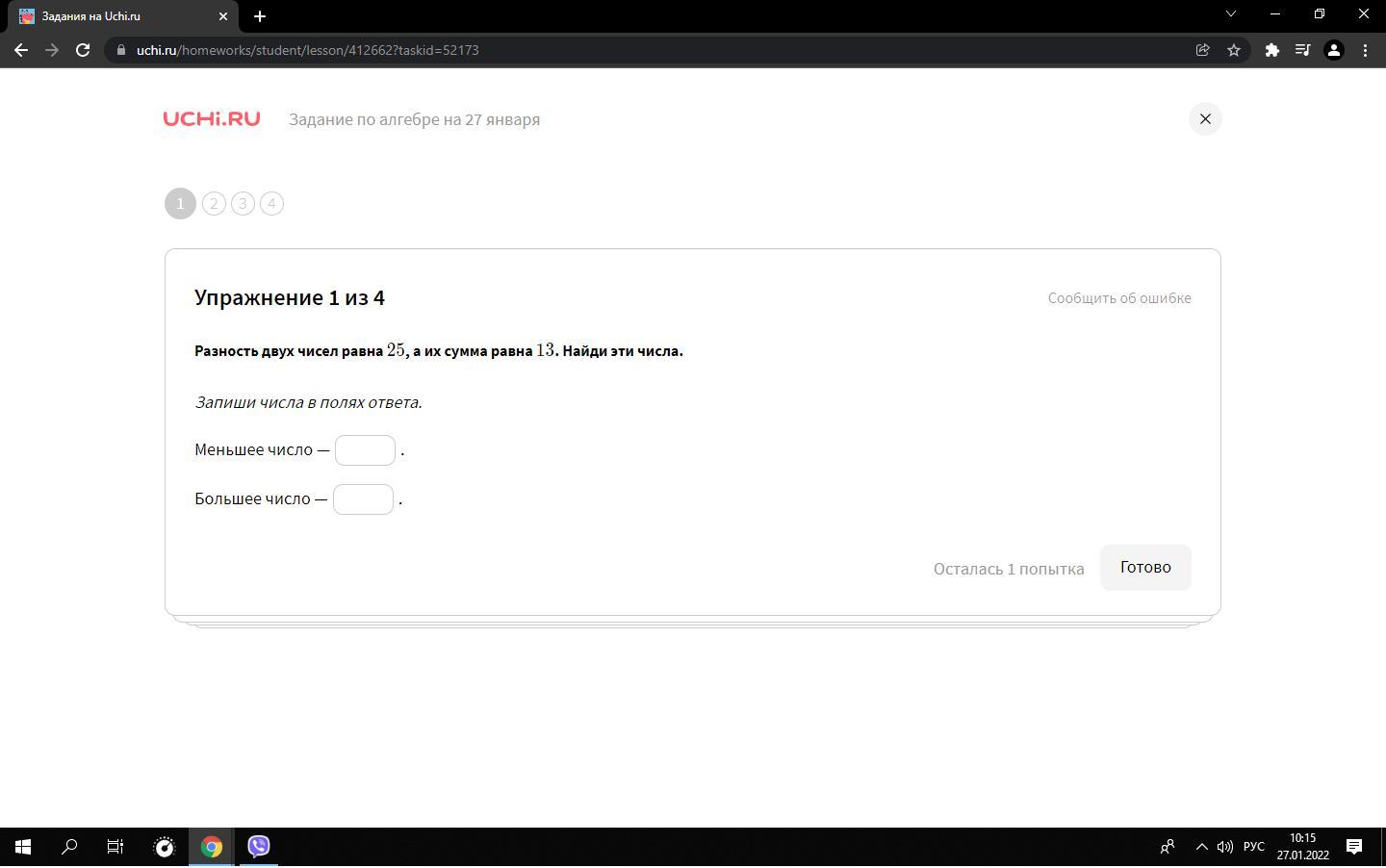
1.
Отметим числа как x и y
Подставим первое значение x
Меньшее -6, большее 19
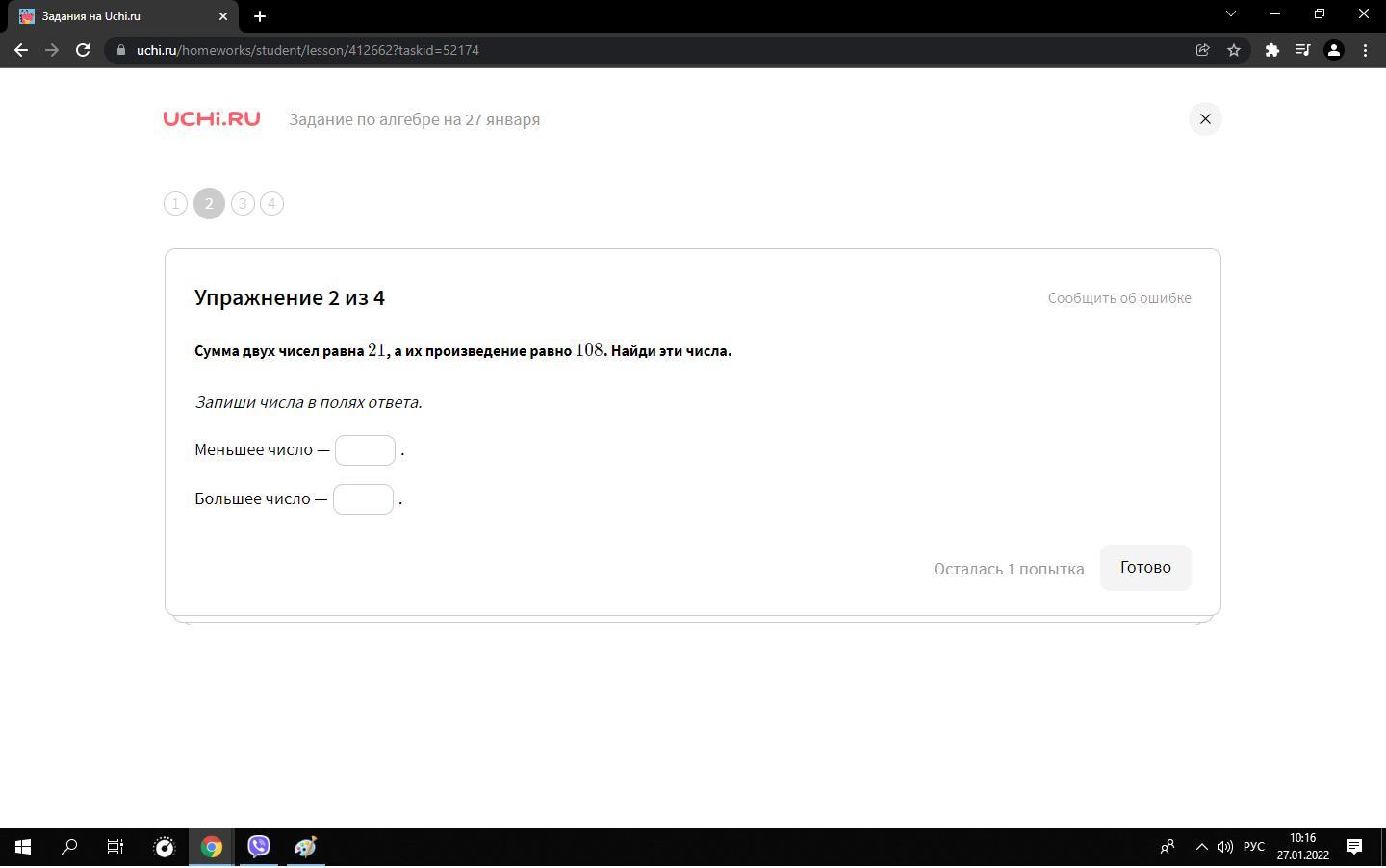
2.
Меньшее 9, большее 12
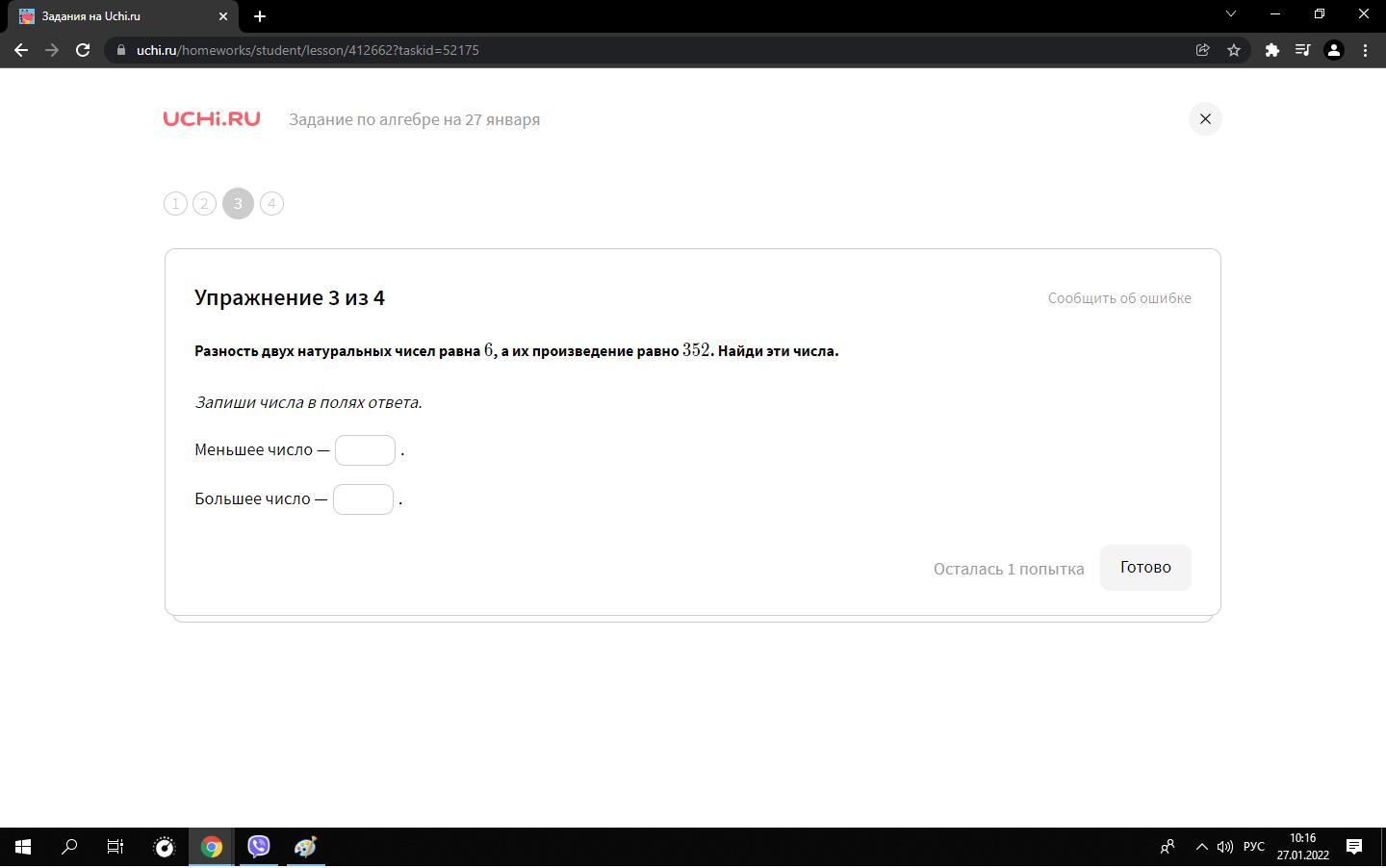
3.
-22 отпадает, потому что говорится, что оба натуральные числа. Натуральные — целые числа больше нуля.
Большее 22, меньшее 16
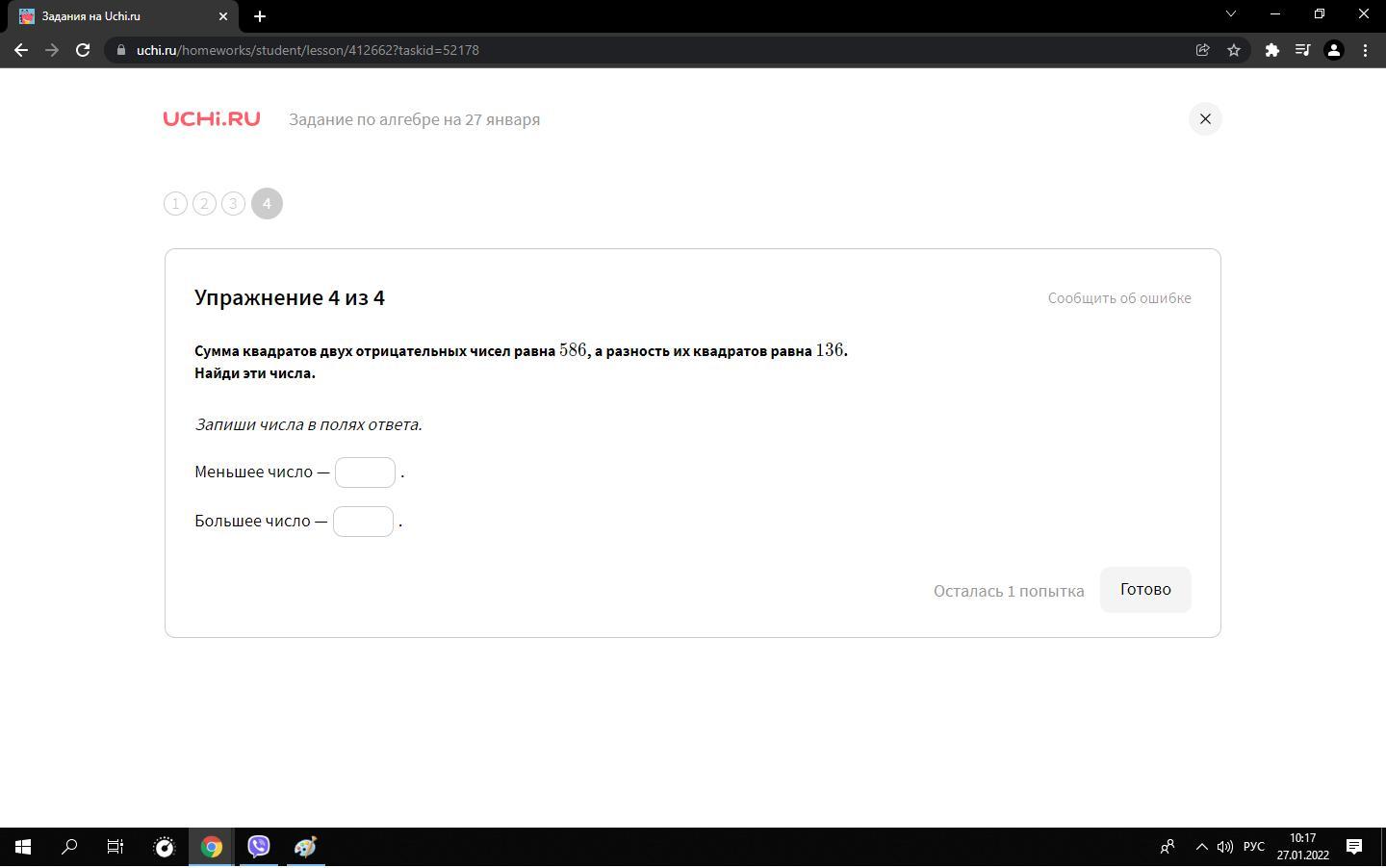
4.
Мы не взяли +15, потому что в условии оба числа отрицательные
Меньшее -19, большее -15
kqoijjjgeye998988:
Дай я тебя поцелую!
Новые вопросы