Математика, вопрос задал Ternov21 , 6 лет назад

Помогите пожалуйста..​

Приложения:
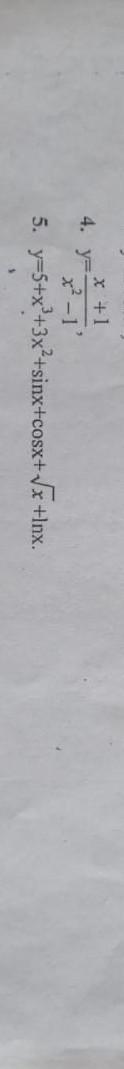
Ternov21: Задание вычислить производные функции

Ответы на вопрос

Ответил natalyabryukhova
1

Пошаговое объяснение:

4.

\displaystyle \left(\frac{u}{v}\right)'= \frac{u'v-uv'}{v^2}

\displaystyle y=\frac{x+1}{x^2-1} \\\\y'=\frac{1*(x^2-1)-(x+1)*2x}{(x^2-1)^2} =\frac{x^2-1-2x^2-2x}{(x^2-1)^2}=-\frac{x^2+2x+1}{y}=\\\\=-\frac{(x+1)^2}{(x^2-1)^2} =-\frac{(x+1)^2}{(x-1)^2*(x+1)^2}=-\frac{1}{(x-1)^2}

Можно сделать проще по формуле:

\displaystyle \left(\frac{1}{v}\right)'=-\frac{v'}{v^2}

\displaystyle y=\frac{x+1}{x^2-1}=\frac{x+1}{(x-1)(x+1)}=\frac{1}{x-1} \\\\y'=-\frac{1}{(x-1)^2} *(x-1)'=-\frac{1}{(x-1)^2}

5.

\displaystyle y=5+x^3+3x^2+sin\;x+cos\;x+\sqrt{x} +ln\;x

Здесь табличные производные:

\displaystyle y'=0+3x^2+3*2x+cos\;x-sin\;x+\frac{1}{2\sqrt{x} } +\frac{1}{x}=\\\\= 3x^2+6x+cos\;x-sin\;x+\frac{1}{2\sqrt{x} } +\frac{1}{x}

Приложения:
Предыдущий вопрос
Следующий вопрос
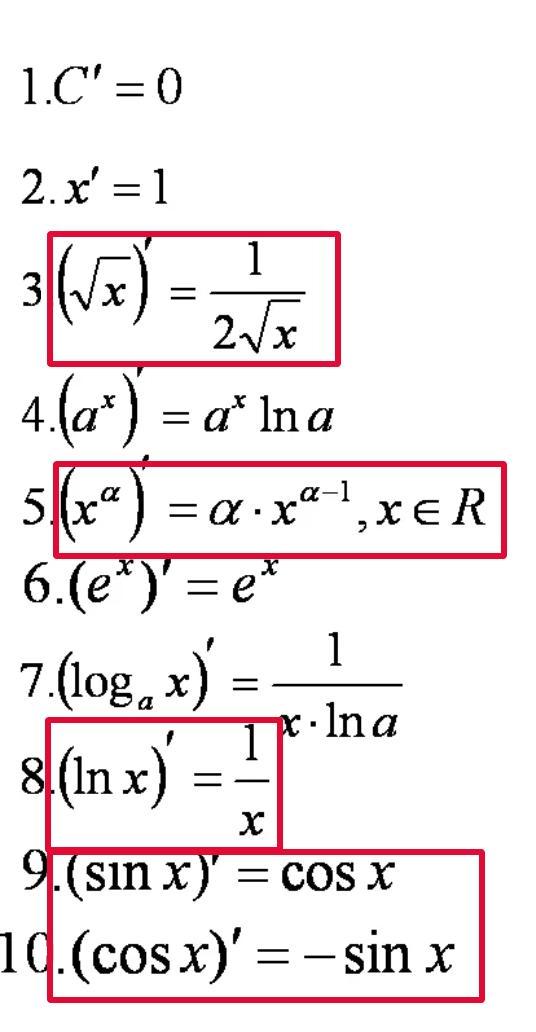
Новые вопросы
Русский язык, 1 год назад
сочинение про свою комнату в художественном стиле...
Английский язык, 1 год назад
как будет данил по английскому...
Биология, 6 лет назад
ПОЖАЛУЙСТА ПОМОГИТЕ!!!! Завтра зачёт(((((...
Обществознание, 6 лет назад
1 и 2 задачи плиз 20 балов Общество...
Геометрия, 8 лет назад
Дано (рисунок 127, а) : угол 1= углу 2, угол 3= 90°. Докажите, что угол 4 - прямой...
История, 8 лет назад
Примеры связи русской культуры с греческой и римской (например: герб России)...