Алгебра, вопрос задал btstaetae997 , 6 лет назад

ПОМОГИТЕ ПОЖАЛУЙСТА!

Приложения:

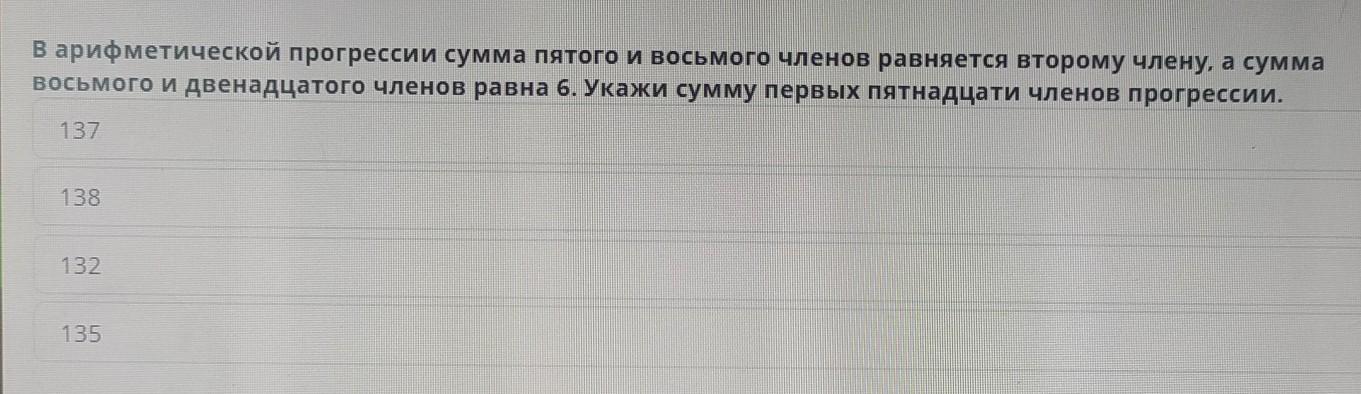
Ответы на вопрос

Ответил zinaidazina

1

Дано:

{ $a_n$ }

$a_5+a_8=a_2$

$a_8+a_{12}=6$

Найти: $S_{15}$

Решение.

1) Выполним преобразования с помощью формулы $a_n=a_1+(n-1)d$ :

а) для первого уравнения

$a_5+a_8=a_2$

$(a_1+4d)+(a_1+7d)=(a_1+d)$

$a_1+10d=0$

б) для второго уравнения

$a_8+a_{12}=6$

$(a_1+7d)+(a_1+11d)=6$

$2a_1+18d=6$ (разделим обе части на 2)

$a_1+9d=3$

2) Получили систему:

$\left \{ {{a_1+10d=0} \atop {a_1+9d=3}} \right.$

Из первого уравнения вычтем второе:

$a_1+10d-(a_1+9d)=0-3$

$a_1+10d-a_1-9d=-3$

$d=-3$

3) В уравнение $a_1+10d=0$ подставим $d=-3$ и найдём $a_1$

$a_1+10*(-3)=0$

$a_1=30$

4) $S_n=\frac{2a_1+(n-1)d}{2}*n$

$S_{15}=\frac{2*30+(15-1)*(-3)}{2}*15= \frac{60-14*3}{2}*15=\frac{18}{2}*15=9*15=135$

$S_{15}=135$

Ответ: 135.

zinaidazina: Спасибо!

btstaetae997: пожалуйста

btstaetae997: помогите с последним вопросом

btstaetae997: пожалуйста

btstaetae997: помогите с последними вопросами

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Английский язык, 1 год назад

чем отличаются read от reading?

Қазақ тiлi, 1 год назад

Архаизмдер мен Тарихи создерге сойлем...

Українська мова, 6 лет назад

Визначте, до яких частин мови належать слова. Розподіліть слова в три колонки: іменники, прикметники, числівники Один, одиниця, одинак, одинокий, одноденний, одинець, одинарний, перший, першість,...

Математика, 6 лет назад

3. Переведите периодическую десятичную дробь в обыкновенную: а) 0.(15) 6) 2.2(1) и запишите решение.

История, 8 лет назад

Что из перечисленного не относится к абсолютизму? 1) утверждается единое общегосударственное законодательство 2) проводится единая экономическая политика 3) король отказывается от попыток...

Геометрия, 8 лет назад

1. Найти площадь заштрихованной части прямоугольника, еслиа = 4 см; b = 3 см; r = 0,8 см; π ≈ 3. 2. Длина окружности цирковой арены равна 42м. Найти диаметр и площадь арены. Число π округлите до...