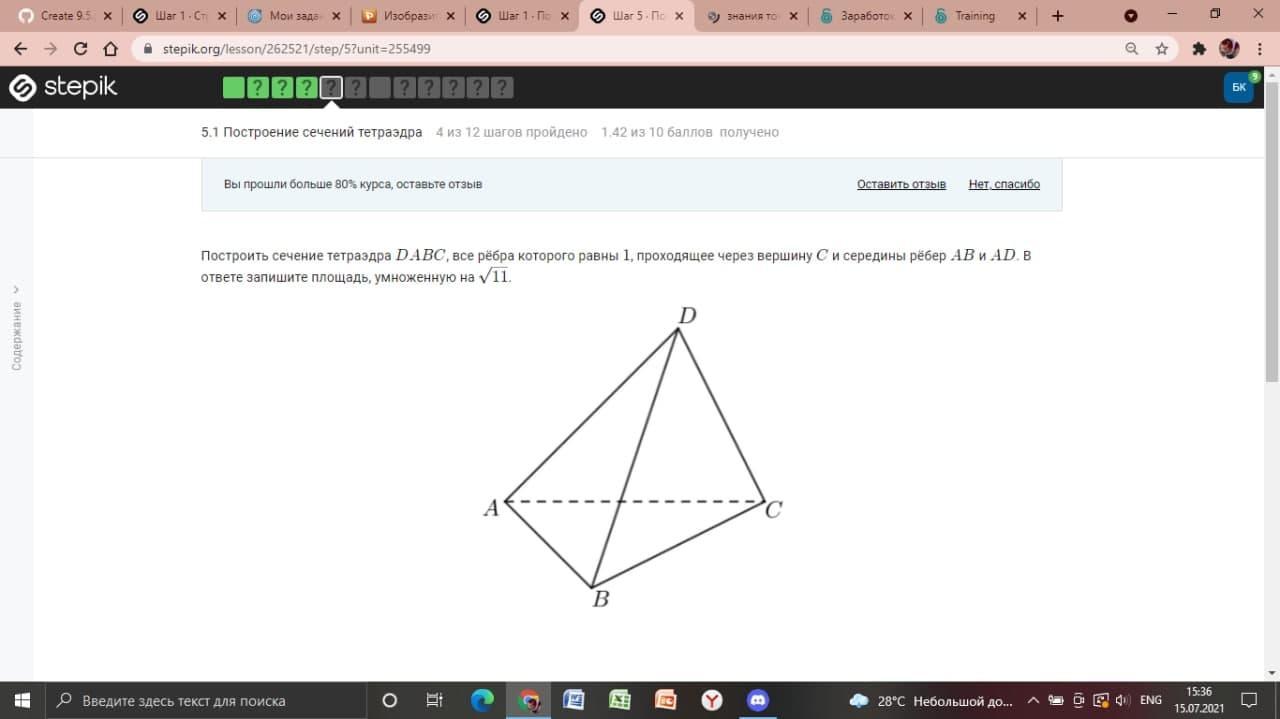
помогите, пожалуйста

Ответ:

1/16.

Пошаговое объяснение:

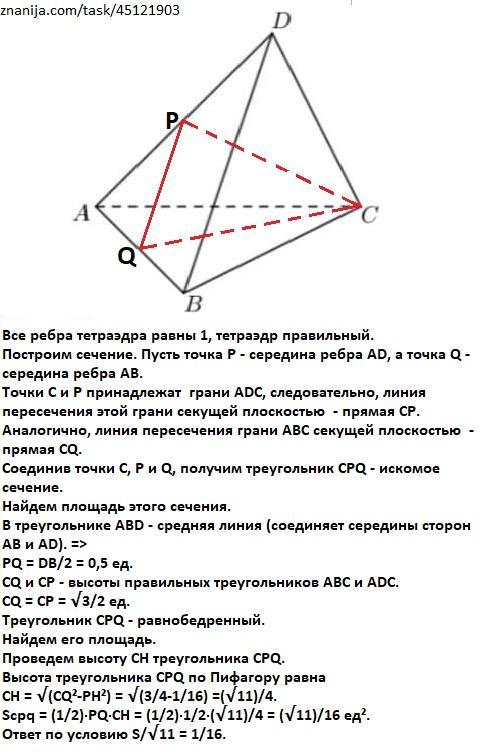
Все ребра тетраэдра равны 1, тетраэдр правильный.

Построим сечение. Пусть точка Р - середина ребра AD, а точка Q - середина ребра AB.

Точки С и Р принадлежат  грани ADC, следовательно, линия пересечения этой грани секущей плоскостью  - прямая СР. Аналогично, линия пересечения грани АВС секущей плоскостью  - прямая СQ.

Соединив точки С, Р и Q, получим треугольник CPQ - искомое сечение.

Найдем площадь этого сечения.

В треугольнике АВD - средняя линия (соединяет середины сторон АВ и АD). =>

PQ = DB/2 = 0,5 ед.

CQ и CP - высоты правильных треугольников АВС и ADC.

CQ = CP = √3/2 ед.

Треугольник CPQ - равнобедренный.

Найдем его площадь.

Проведем высоту СН треугольника СРQ.

Высота треугольника CPQ по Пифагору равна  

CH = √(CQ²-PH²) = √(3/4-1/16) =(√11)/4.

Scpq = (1/2)·PQ·CH = (1/2)·1/2·(√11)/4 = (√11)/16 ед².

Ответ по условию S/√11 = 1/16.