Помогите пожалуйста
Приложения:

Ответы на вопрос
Ответил NNNLLL54
1
Ответ:
Приложения:
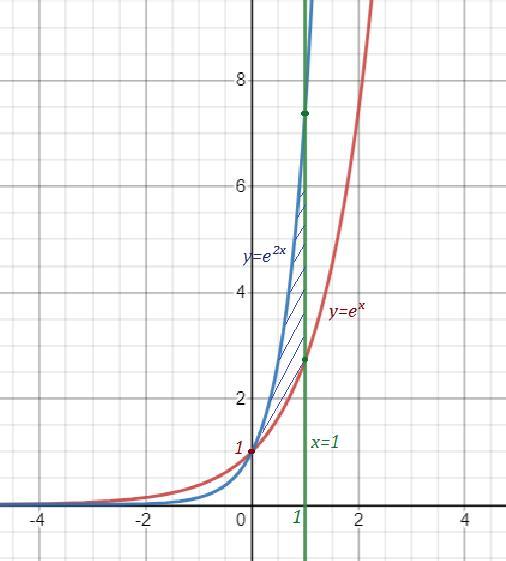
Новые вопросы
Английский язык,
1 год назад
Окружающий мир,
1 год назад
Математика,
2 года назад
Русский язык,
2 года назад
• главный мозг
• 34.1 тыс. ответов
• 185.8 млн пользователей, получивших помощь
https://znanija.com/app/profile/1385058