Помогите пожалуйста .4.

Ответы на вопрос
ОТВЕТ: АН=9,6 ед.
ЗАДАЧА
В равнобедренном треугольнике боковая сторона 10, а основание 12. Найдите высоту треугольника, проведенную к боковой стороне.
ДАНО:
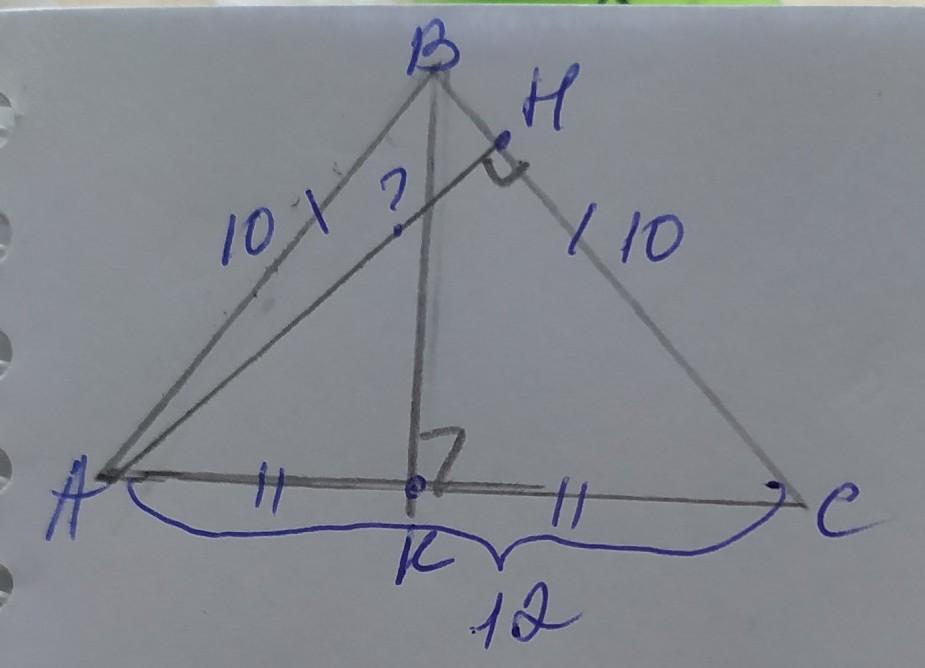
∆АВС; АВ=ВС=10; АС=12; АН – высота.
НАЙТИ: АН
=====================================
РЕШЕНИЕ:
проведем высоту ВК к основанию АС. Так как ∆АВС равнобедренный, то ВК является также медианой и делит основание АС пополам, поэтому АК=СК=12÷2=6(ед.)
Рассмотрим ∆АВК, он прямоугольный где АК и ВК – катеты, а АВ – гипотенуза. найдём высоту ВК, используя теорему Пифагора:
ВК²+АК²=АВ² → ВК²=АВ²–АК²=10²–6²=100–36=64
ВК=√64=8(ед.)
Площадь (S) треугольника равна полупроизведению его высоты, проведенной к одной из его строн, формула:
Sabc=(AC•BK):2=(12•8)÷2=48(ед²)
Используя эту формулу найдём высоту АН, применив данные стороны ВС:
(BC•AH):2=S
(10•AH)÷2=48
10•AH=48•2
10•AH=96
AH=96÷10
AH=9,6(ед.)