помогите пожалуйста!!!
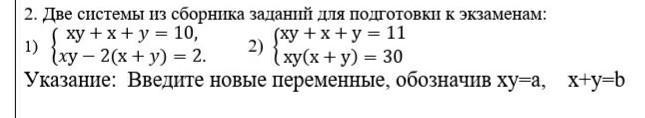
Ответы на вопрос
Ответ:
В решении.
Объяснение:
Решить системы уравнений.
1) ху +х+у=10
ху-2(х+у)=2
Ввести новые переменные:
ху=а; (х+у)=b.
a+b=10
a-2b=2
Выразить а через b в первом уравнении, подставить выражение во второе уравнение и вычислить b:
a=10-b
10-b-2b=2
-3b= -8
b= -8/-3
b=8/3= 2 и 2/3;
а=10 - 2 и 2/3
а= 7 и 1/3 = 22/3.
Возвращаемся к первоначальным переменным:
ху=22/3;
х+у=8/3.
Выразить х через у:
х=22/3у
х=8/3-у
Приравнять правые части уравнений (левые равны) и вычислить у:
22/3у=8/3-у
Умножить уравнение на 3у, чтобы избавиться от дроби:
22=8у-3у²
3у²-8у+22=0, квадратное уравнение, ищем корни:
D=b²-4ac =64-264= -200 √D < 0, уравнение не имеет действительных корней.
у₁=(-b-√D)/2a
у₂=(-b+√D)/2a
2)ху+х+у=11
ху(х+у)=30
Ввести новые переменные:
ху=а; (х+у)=b.
a+b=11
ab=30
Выразить а через b в первом уравнении, подставить выражение во второе уравнение и вычислить b:
a=11-b
(11-b)*b=30
11b-b²=30
-b²+11b-30=0/-1
b²-11b+30=0, квадратное уравнение, ищем корни:
D=b²-4ac =121-120=1 √D= 1
b₁=(-b-√D)/2a
b₁=(11-1)/2
b₁=5;
b₂=(-b+√D)/2a
b₂=(11+1)/2
b₂=6.
a₁= 11-b₁
a₁= 11-5
a₁= 6;
a₂=11-b₂
a₂=11-6
a₂=5.
Возвращаемся к первоначальным переменным:
1) ху=a₁= 6; х+у=b₁=5;
Выразить х через у в первом уравнении, подставить выражение во второе уравнение и вычислить у:
х=6/у
х+у=5
6/у+у=5
Умножить уравнение на у, чтобы избавиться от дроби:
6+у²=5у
у²-5у+6=0, квадратное уравнение, ищем корни:
D=b²-4ac =25-24=1 √D=1
у₁=(-b-√D)/2a
у₁=(5-1)/2
у₁=2;
у₂=(-b+√D)/2a
у₂=(5+1)/2
у₂=3;
х=6/у
х₁=6/у₁
х₁=6/2
х₁=3;
х₂=6/у₂
х₂=6/3
х₂=2.
2)ху=a₂=5; х+у=b₂=6.
Выразить х через у в первом уравнении, подставить выражение во второе уравнение и вычислить у:
х=5/у
5/у+у=6
Умножить уравнение на у, чтобы избавиться от дроби:
5+у²=6у
у²-6у+5=0, квадратное уравнение, ищем корни:
D=b²-4ac =36-20=16 √D= 4
у₃=(-b-√D)/2a
у₃=(6-4)/2
у₃=1;
у₄=(-b+√D)/2a
у₄=(6+4)/2
у₄=5;
х=5/у
х₃=5/у₃
х₃=5/1
х₃=5;
х₄=5/у₄
х₄=5/5
х₄=1.
Решение системы уравнений (3; 2); (2; 3); (5; 1); (1; 5).
Проверка путём подстановки вычисленных значений х и у в систему уравнений показала, что данное решение удовлетворяет данной системе уравнений.