Алгебра, вопрос задал Аноним , 1 год назад

ПОМОГИТЕ ПОЖАЛУЙСТА.

Приложения:

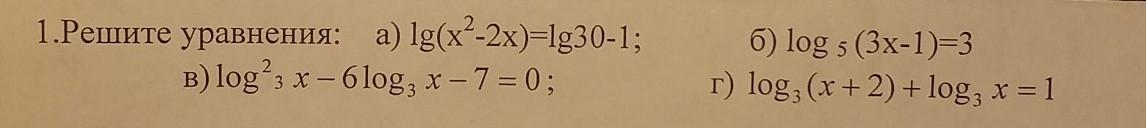
Ответы на вопрос

Ответил NNNLLL54

1

$1)\; \; lg(x^2-2x)=lg30-1\\\\ODZ:\; \; x^2-2x>0\; ,\; x(x-2)>0\; \; ,\; \; x\in (-\infty ,0)\cup 2,+\infty )\\\\lg(x^2-2x)=lg30-lg10\\\\x^2-2x=3\; \; ,\; \; x^2-2x-3=0\; \; ,\; \; x_1=-1\; ,\; x_2=3\; \; (teorema\; Vieta)\\\\Otvet:\; \; x_1=-1\; ,\; x_2=3\; .$

$2)\; \; log_5(3x-1)=3\; ,\; \; ODZ:\; \; 3x-1>0\; ,\; \; x>\frac{1}{3}\\\\log_5(3x-1)=log_55^3\\\\3x-1=125\; \; ,\; \; 3x=126\; ,\; \; x=67\\\\Otvet:\; \; x=67\; .$

$3)\; \; log_3^2x-6log_3x-7=0\; \; ,\qquad ODZ:\; x>0\\\\t=log_3x\; ,\; \; t^2-6t-7=0\; ,\; \; t_1=-1\; ,\; t_2=7\; \; (teorema\, \; Vieta)\\\\log_3x=-1\; \; ,\; \; x=3^{-1}=\frac{1}{3}\\\\log_3x=7\; \; ,\; \; x=3^7=2187\\\\Otvet:\; \; x_1=\frac{1}{3}\; \; ,\; \; x_2=2187\; .$

$4)\; \; log_3(x+2)+log_3x=1\; \; ,\; \; \; ODZ:\; \; x>0\\\\log_3(x+2)+log_3x=log_33\\\\x(x+2)=3\; \; ,\; \; x^2+2x-3=0\; ,\; \; x_1=-3<0\; ,\; x_2=1\; \; (teorema\; Vieta)\\\\Otvet:\; \; x=1\; .$

NNNLLL54: если не видишь текст, перезагрузи страницу...

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Українська мова, 1 год назад

1. Завтра вранці вийде сонце (О. Роговенко).2. Сонце лагідно знову всміхається(Н. Бідненко). 3. Світ мені усміхається тепло (П. Перебийніс). 4. Сонцепосміхнулося здаля (Д. Павличко). Гроза...

Алгебра, 1 год назад

Перший член геометричної прогресії знаменник b1= - 1/27 , а знаменник g=-3. Знайдіть b3 .

История, 1 год назад

Чем отличаются древние олимпийские игры от современных...

Математика, 1 год назад

3. Задание 3 № 251003. Найдите (в см?) площадь S фигуры, изображенной на клетчатой бумаге с размером клетки 1 см X 1 см (см. рис.). В ответе запишите — S/П ...

Математика, 6 лет назад

для того чтобы связать свитер хозяйке нужно 800 граммов шерстяной пряжи синего цвета. можно купить синюю пряжу по цене 84 руб. за 100 г а можно купить неокрашенную пряжу за 76 руб за 100 г и окрасить...

Русский язык, 6 лет назад

Как пишется слово веселится с мягким знаком или без?помогите срочно!