помогите, пожалуйста )
Приложения:
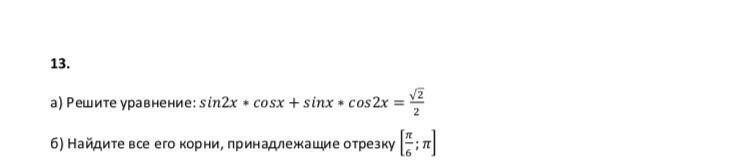
Ответы на вопрос
Ответил nafanya2014
0
Формула синуса суммы:
sinα·cosβ+cosαsinβ=sin(α+β)
Уравнение:
sinx(2x+x)=(√2)/2
sin3x=(√2)/2
3x=(-1)ⁿarcsin((√2)/2)+π·n, n∈Z
3x=(-1)ⁿ(π/4)+π·n, n∈Z,
x=(-1)ⁿ(π/12)+(π/3)·n, n∈Z
О т в е т.
a)
-1)ⁿ(π/12)+(π/3)·n, n∈Z
б)
(π/4);(2π/3); (3π/4);
При
n=0
x=(π/12)∉[π/6;π]
При
n=1
-(π/12)+(π/3)·1=3π/12=(π/4)∈[π/6;π]
При
n=2
(π/12)+(π/3)·2=9π/12=(3π/4)∈[π/6;π]
При
n=3
-(π/12)+(π/3)·3=8π/12=(2π/3)∈[π/6;π]
Новые вопросы
Русский язык,
1 год назад
Русский язык,
1 год назад
Математика,
7 лет назад
Математика,
8 лет назад
Математика,
8 лет назад