ПОМОГИТЕ ПОЖАЛУЙСТА, 20 МИНУТ
Приложения:
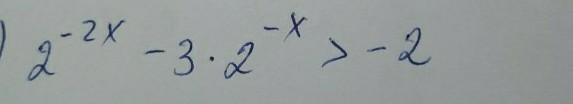
Ответы на вопрос
Ответил bb573878
2
Ответ:
Объяснение:
Ответил zveryakovanata
1
Ответ:
Объяснение: (2⁻ˣ)² -3· (2⁻ˣ)+2>0
пусть (2⁻ˣ)=у, тогда неравенство примет вид:
у²-3у+2>0
D= 9-8=1
y₁=(3+1)/2=2
y₂=(3-1)/2=1
График функции f(y)=у²-3у+2 -парабола, направленная ветвями вверх и пересекающая горизонтальную ось Оу в точках 1 и 2 ⇒ f(y)>0 , если у<1 и у>2
Тогда, если
a) у<1, то (2⁻ˣ)<1
(2⁻ˣ)<2⁰
основание показательной функции 2>1, значит функция возрастающая ⇒ -x<0
x>0 x∈(0;∞)
б) у>2, то (2⁻ˣ)>2
(2⁻ˣ)<2¹
основание показательной функции 2>1, значит функция возрастающая ⇒
-x>1
x< -1 ⇒x∈(-∞;-1)
Ответ: (-∞;-1)∪(0;∞)
Новые вопросы
Русский язык,
1 год назад
Другие предметы,
1 год назад
Английский язык,
6 лет назад
Геометрия,
8 лет назад