ПОМОГИТЕ ПОЖАЛУЙСТА
1. Знайдіть область визначення функції: у = (3 бали) x-31
2. Дослідіть на парність і непарність функцію у = x³ - х. (3 бали)
3. Побудуйте графік функцiї: 20 a) y=√x+4-2 (3 бали) б) у = |x|3 - 1 (3 бали) =
Приложения:
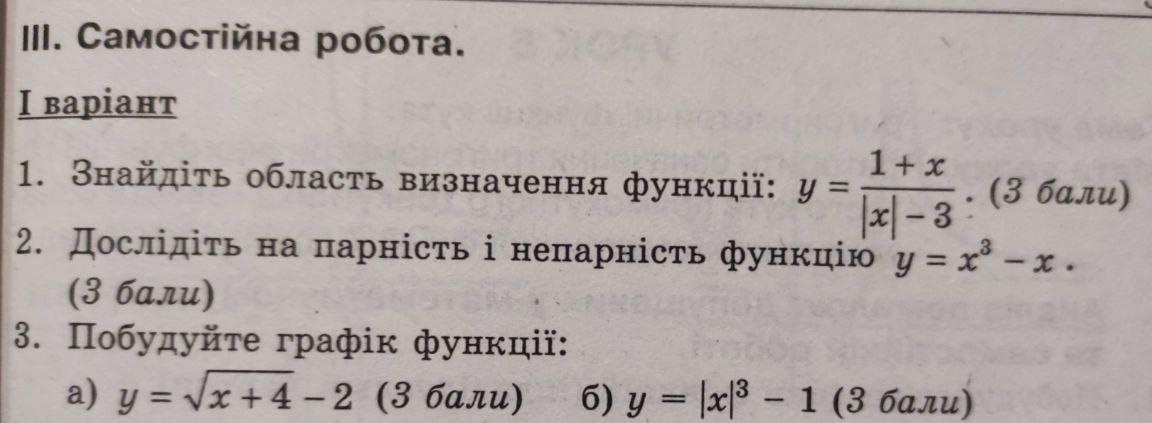
Ответы на вопрос
Ответил bibika6179
2
1. Область визначення функції у = x - 31
Функція у = x - 31 не має обмежень в області визначення x, тобто може приймати будь-які значення x. Тобто область визначення цієї функції - це усі дійсні числа.
2. Дослідження на парність і непарність функції у = x³ - x
Щоб дослідити функцію на парність і непарність, перевіримо, як вона веде себе при виконанні умов -f(x) = f(-x) для парної функції і f(x) = -f(-x) для непарної функції.
-f(x) = -(x³ - x) = -x³ + x
f(-x) = (-x)³ - (-x) = -x³ + x
Ми бачимо, що -f(x) = f(-x), тобто функція у = x³ - x є парною.
3. Побудова графіку функції:
а) y = √(x + 4) - 2
Графік цієї функції виглядає як корінь зі зсунутою вниз на 2 одиниці функції y = √x. Графік проходить через точку (-4, -2) і росте при збільшенні x.
б) у = |x|³ - 1
Графік цієї функції виглядає як модуль куба x зі зсунутою вниз на 1 одиницю. Графік є симетричним відносно вісі y і проходить через точку (0, -1). Усі значення функції більше або рівні -1.
Для побудови графіків можна використовувати графічний програмний засіб або графічний калькулятор.
Функція у = x - 31 не має обмежень в області визначення x, тобто може приймати будь-які значення x. Тобто область визначення цієї функції - це усі дійсні числа.
2. Дослідження на парність і непарність функції у = x³ - x
Щоб дослідити функцію на парність і непарність, перевіримо, як вона веде себе при виконанні умов -f(x) = f(-x) для парної функції і f(x) = -f(-x) для непарної функції.
-f(x) = -(x³ - x) = -x³ + x
f(-x) = (-x)³ - (-x) = -x³ + x
Ми бачимо, що -f(x) = f(-x), тобто функція у = x³ - x є парною.
3. Побудова графіку функції:
а) y = √(x + 4) - 2
Графік цієї функції виглядає як корінь зі зсунутою вниз на 2 одиниці функції y = √x. Графік проходить через точку (-4, -2) і росте при збільшенні x.
б) у = |x|³ - 1
Графік цієї функції виглядає як модуль куба x зі зсунутою вниз на 1 одиницю. Графік є симетричним відносно вісі y і проходить через точку (0, -1). Усі значення функції більше або рівні -1.
Для побудови графіків можна використовувати графічний програмний засіб або графічний калькулятор.
Новые вопросы
Алгебра,
11 месяцев назад
Окружающий мир,
11 месяцев назад
Физика,
11 месяцев назад
Математика,
6 лет назад
Алгебра,
6 лет назад