Алгебра, вопрос задал OneMan2019 , 1 год назад

Помогите потенцировать надо

Приложения:

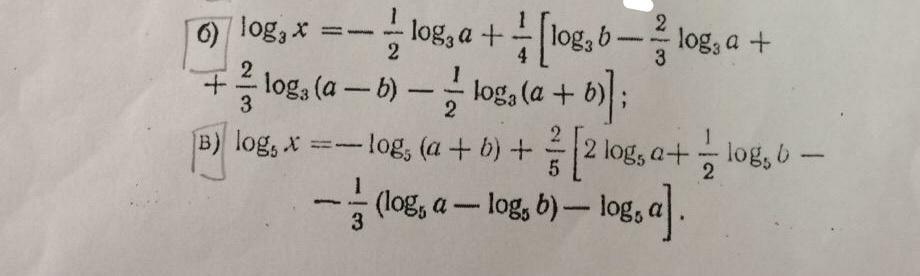
Ответы на вопрос

Ответил tamarabernukho

Ответ:

Объяснение:

Если по данному результату логарифмирования находят выражение,

от которого получен этот результат, то такую операцию называют

потенцированием.

Приложения:

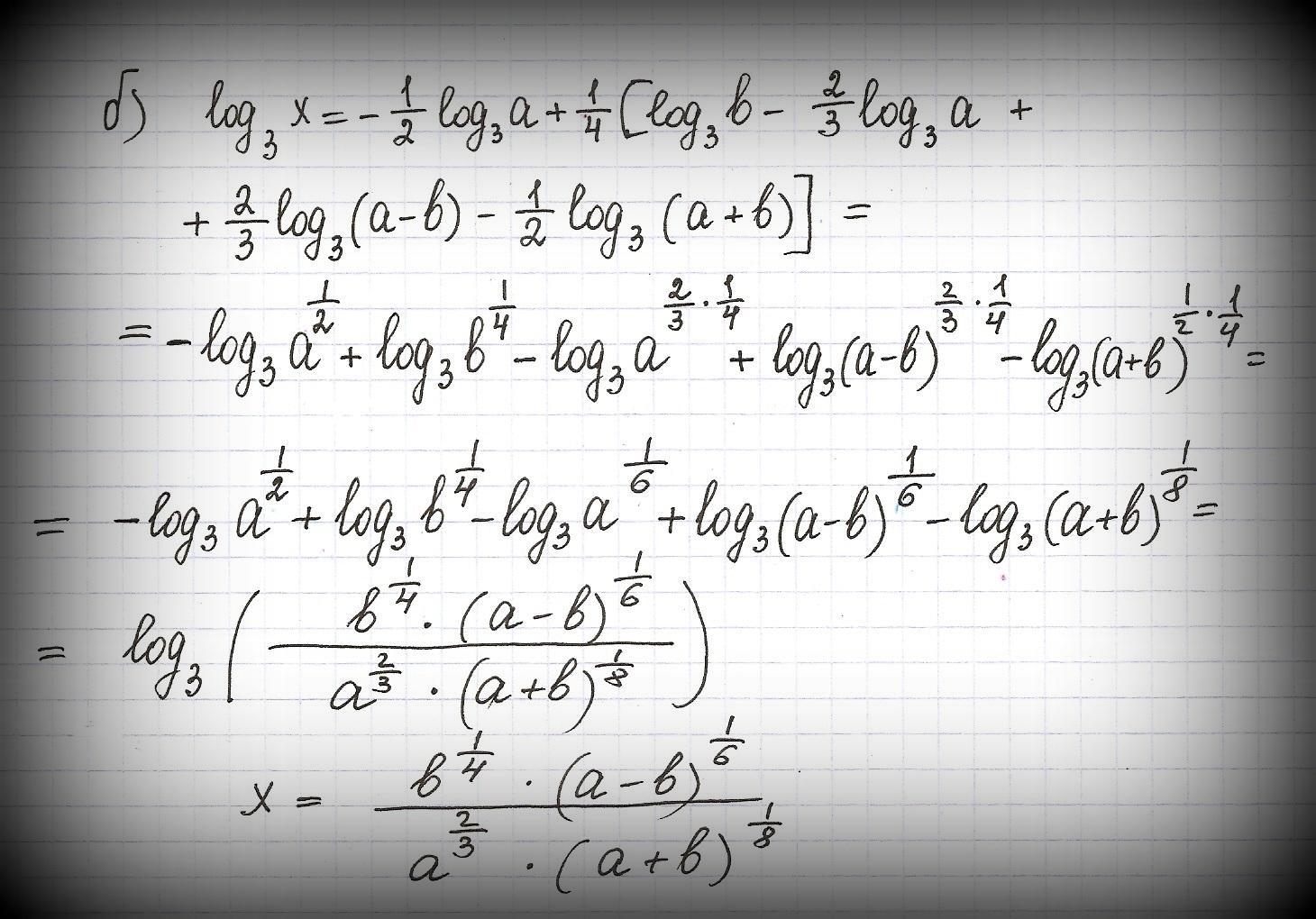
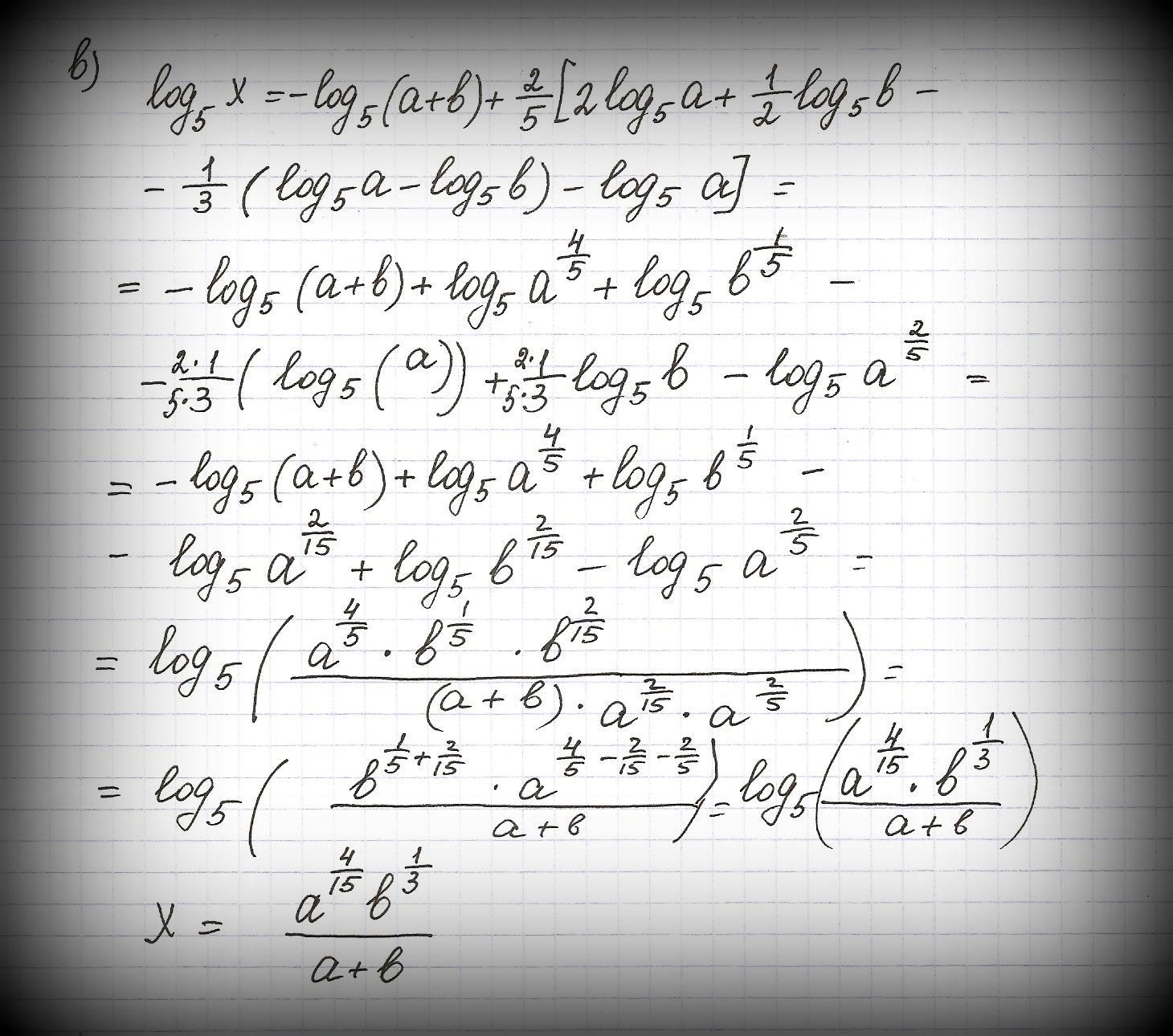
Ответил NNNLLL54

$1)\; log_3x=-\frac{1}{2}\, log_3a+\frac{1}{4}\Big (log_3b-\frac{2}{3}\, log_3a+\frac{2}{3}\, log_3(a-b)-\frac{1}{2}\, log_3(a+b)\Big )\\\\log_3x=-\frac{1}{2}\, log_3a+\frac{1}{4}\, log_3b-\frac{1}{6}\, log_3a+ \frac{1}{6}\, log_3(a-b)-\frac{1}{8}\, log_3(a+b)\\\\log_3x=-log_3a^{\frac{1}{2}}+\log_3b^{\frac{1}{4}}-log_3a^{\frac{1}{6}}+log_3(a-b)^{\frac{1}{6}}-log_3(a+b)^{\frac{1}{8}}\\\\log_3x=log_3\; \frac{b^{\frac{1}{4}}\cdot (a-b)^{\frac{1}{6}}}{a^{\frac{1}{2}}\cdot a^{\frac{1}{6}}\cdot (a+b)^{\frac{1}{8}}}$

$x=\frac{b^{\frac{1}{4}}\cdot (a-b)^{\frac{1}{6}}}{a^{\frac{1}{2}}\cdot a^{\frac{1}{6}}\cdot (a+b)^{\frac{1}{8}}}\\\\x=\frac{b^{\frac{1}{4}}\cdot (a-b)^{\frac{1}{6}}}{a^{\frac{2}{3}}\cdot (a+b)^{\frac{1}{8}}}$

$2)\; \; log_5x=-log_5(a+b)+\frac{2}{5}\Big (2\, log_5a+\frac{1}{2}\, log_5b-\frac{1}{3}\, (log_5a-log_5b)-log_5a\Big )\\\\ log_5x=-log_5(a+b)+\frac{4}{5}\, log_5a+\frac{1}{5}\, log_5b-\frac{2}{15}\, log_5a+\frac{2}{15}\, log_5b-\frac{2}{5}\, log_5a\\\\log_5x=-log_5(a+b)+log_5a^{\frac{4}{5}}+log_5b^{\frac{1}{5}}-log_5a^{\frac{2}{15}}+log_5b^{\frac{2}{15}}-log_5a^{\frac{2}{5}}\\\\log_5x=log_5\; \frac{a^{\frac{4}{5}}\cdot b^{\frac{1}{5}}\cdot b^{\frac{2}{15}}}{(a+b)\cdot a^{\frac{2}{15}}\cdot a^{\frac{2}{5}}}\\\\x=\frac{a^{\frac{4}{5}}\cdot b^{\frac{1}{5}}\cdot b^{\frac{2}{15}}}{(a+b)\cdot a^{\frac{2}{15}}\cdot a^{\frac{2}{5}}}\\\\x=\frac{a^{\frac{4}{15}}\cdot b^{\frac{1}{3}}}{a+b}$

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Немецкий язык, 1 год назад

Будь ласка , допоможіть зробить, дам бали...

Английский язык, 1 год назад

FIND 11 WORDS Помогите кто как пожалуйста ето кр задание здать мне сегодня надо...

Другие предметы, 1 год назад

Здравствуйте всем,нужна помощь по Крымоведению Заполните таблицу,проставив в соответствующие ячейки порядковые номера названий горных пород Осадочные Магматические Метаморфические 1 туф 2...

Русский язык, 1 год назад

ПОмогите пожалуйста!! Замините словосочитание Вошел с улыбкой со связью примыкание Испуганно шептал управление Вошел с улыбкой примыкание Цветок в поле согласование Сказал с насмешкой...

Алгебра, 6 лет назад

Имеет ли нули функция: у = 4х(х - 2);...

Математика, 6 лет назад

Надо сделать трёхзначные числа из 4 9 1 и 6 5 0 с повторениями даю все балы...